5. Weighted Finite-State Transducers
Info
기존 음성 인식 시스템 학습이 끝나고 디코딩 시 여러 경로들에 대한 확률 계산을 빠르고 효율적으로 시행하기 위해 사용하는 Weighted Finite-State Transducers를 살펴본다.
1. Concept
Weighted Finite-State Transducers(WFST)를 개념적으로 나타낸 그림은 그림1과 같다. WFST는 그림1과 같이 노드(node)와 에지(edge)로 구성돼 있는 그래프로 이해할 수 있는데, 동그라미로 표시된 것이 노드이며 상태(state)를 가리킨다. 여기에서는 상태가 시점(time)으로 쓰이고 있다. 노드와 노드를 연결하는 화살표가 에지이며 그 위에 적힌 정보는 입력 레이블 : 출력 레이블 / 스코어이다. 상태들이 유한(finite) 개이며 가중치 정보가 포함돼 있다는 취지에서 WFST라는 이름이 붙은 것 같다.
그림1의 상단은 언어 모델(Language Model)을 WFST로 나타낸 것이다. 언어 모델은 단어 수준에서 학습됐기 때문에 입력 레이블과 출력 레이블 모두 단어로 같고 각 상태에서 다음 상태로 전이할 스코어를 모두 더하면 그 합이 1이 된다(즉 각 스코어는 확률이 됨). 그림1의 상단 WFST가 허용하는 입력 경로(path)는 using data is better, using data are better, …, using intuition is worse 등 12가지이다. WFST는 단어 시퀀스를 입력 받아 그에 대응하는 출력 레이블 시퀀스에 관련된 경로들의 확률합을 리턴하게 된다. WFST는 입력이 주어졌을 때 가능한 모든 출력 경로들에 관련된 확률들을 빠르고 효과적으로 계산해 주는 것이 목적이다.
그림1 MOTIVATION
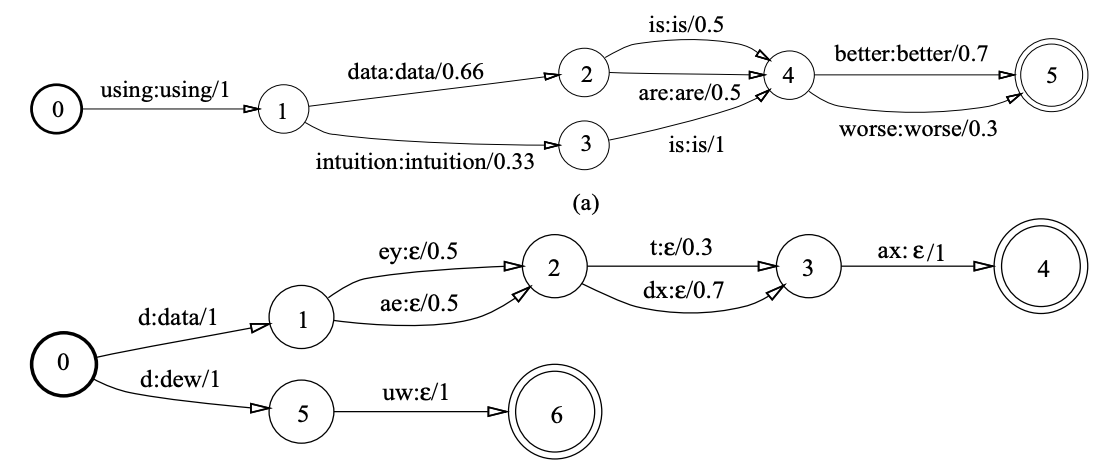
그림2의 하단은 발음사전(pronunciation lexi)을 WFST로 나타낸 것이다. 이 WFST는 출력 레이블은 data라는 단어에 대응되는 입력 레이블 시퀀스는 d ey t ax나 d ey dx ax, d ae t ax, d ae dx ax 등 4가지이다. 출력 레이블 시퀀스 dew라는 단어에 대응하는 입력 레이블 시퀀스는 d ew이다. 이 WFST는 총 5가지의 경로가 나타나 있는데, 첫 번째 에지가 이후 에지 시퀀스의 디코딩 결과를 대변하고 있다. 이와 관련해 두 번째 이후의 전이(transition)는 출력이 모두 \(\epsilon\)(empty)임을 확인할 수 있다.
수식1은 WFST를 수식으로 정리한 것이다. 이를 그림2 하단 예시와 연관지어 생각해 보자. 우선 \(\pi\)는 시작 상태 집합(\(I\)) 가운데 하나 혹은 여럿의 시퀀스로 시작해 종료 상태 집합(\(F\)) 가운데 하나 혹은 여럿의 시퀀스로 끝나되, 입력 시퀀스 \(x\)와 출력 시퀀스 \(y\)에 관계된 경로(path) 가운데 하나이다. 그림2 하단 예시에서 d ey t ax나 d ey dx ax, d ae t ax, d ae dx ax 각각이 \(\pi\)에 해당한다. d ey t ax의 확률은 시작~종료에 이르는 전이 확률들을 모두 곱하면(⨂) 된다. \(1 \times 0.5 \times 0.3 \times 1\)이다. 모든 가능한 경로들의 합(⨁)이 WFST의 최종 결과이므로 d ey t ax, d ey dx ax, d ae t ax, d ae dx ax 네 가지 확률 값들을 모두 더해준다.
수식1 WEIGHTED FINITE-STATE TRANSDUCERS
2. Operations
이번 챕터에서는 WFST의 중요 연산 세 가지를 살펴보도록 한다. WFST에 Composition, Determinization, Minimization 등 연산을 적용하게 되면 탐색 경로가 확 줄어들기 때문에 입력 시퀀스에 대응하는 가능한 모든 경로의 출력 시퀀스와 관련된 확률 합을 효율적으로 계산할 수 있게 된다. 차례대로 살펴보자.
1) Composition
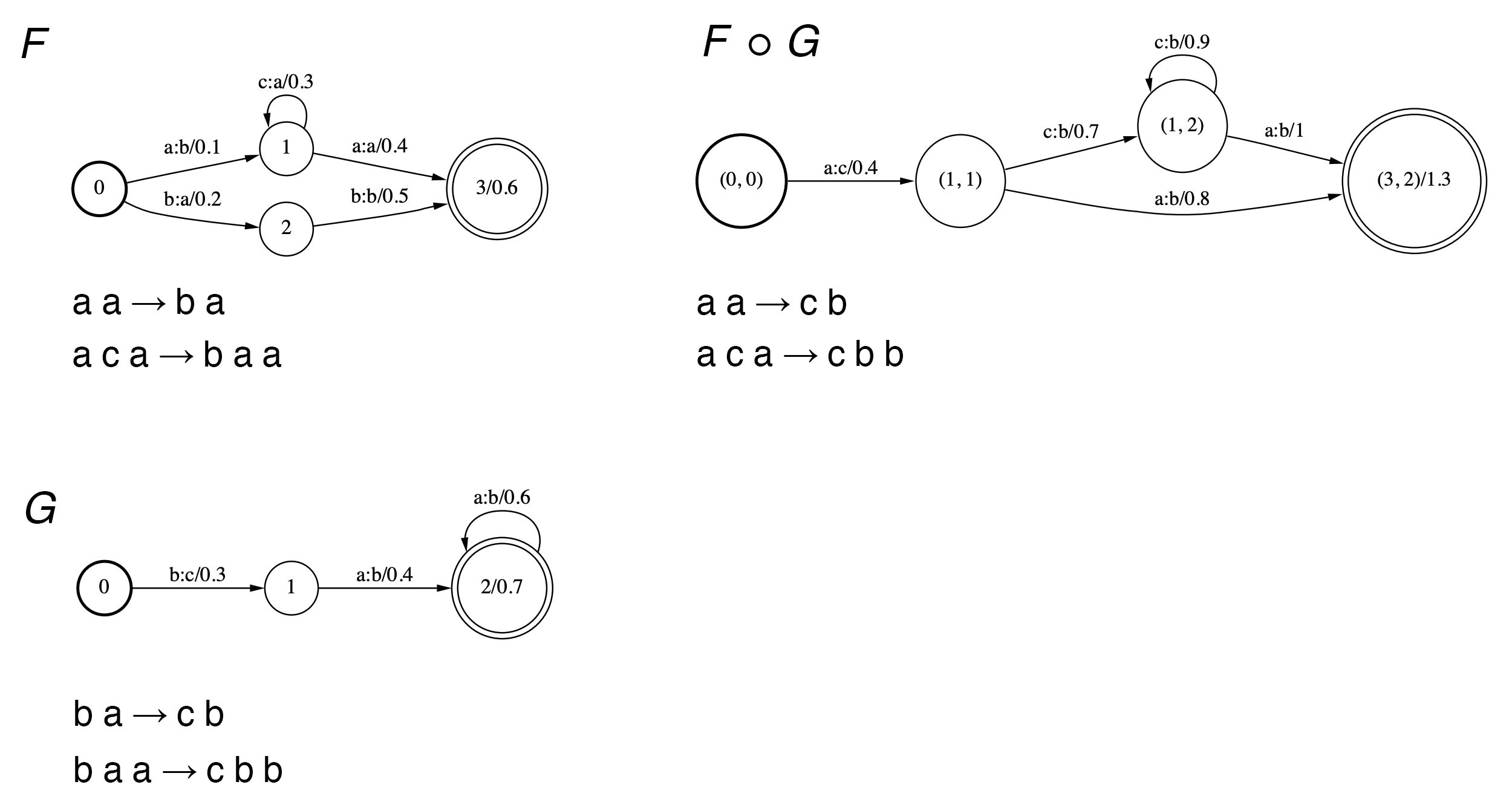
Composition 연산은 두 개의 WFST를 하나로 합성하는 연산이다. 연산 예시는 그림2와 같다. \(F\)와 \(G\)라는 WFST가 주어졌을 때 \(F \circ G\)는 이 둘이 내포하고 있는 모든 경로를 합성한다. 예컨대 \(F\)에는 입력 시퀀스 a a, 출력 시퀀스 b a가 정의되어 있고, \(G\)에는 입력 b a, c b가 있다. 이에 \(F \circ G\)에서는 입력 a a를 출력 c b로 매핑한다.
그림2 COMPOSITION
2) Determinization
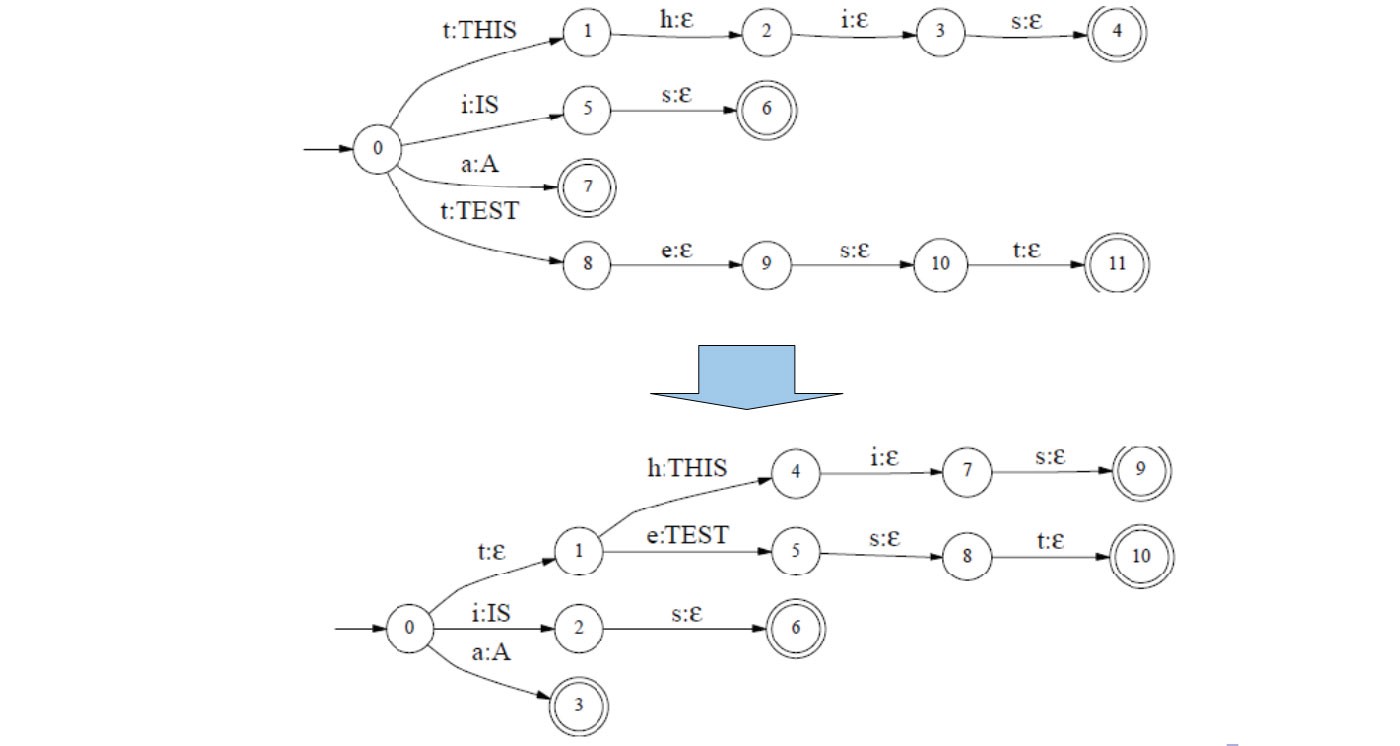
Determinization 연산은 겹치는 복수의 전이(transition)를 하나의 유니크한 전이로 합치는 연산이다. 그림3과 같다. 그림3에서 THIS와 TEST는 음소 t를 입력으로 한다는 점에서 겹친다. 이에 t:ε 에지를 새로 두어 해당 전이를 유니크하게 변환한다.
그림3 DETERMINIZATION
3) Minimization
Minimization 연산은 겹치는 복수의 상태(state)를 합치는 연산이다. 그림4와 같다.
그림4 MINIMIZATION

3. WFST with ASR
우리의 목적은 언어 모델(Language Model, Word-level Grammar), 발음 사전(pronouncitaion lexicon), Context-Dependency, 히든 마코프 모델(Hidden Markov Model) 등 다양한 소스를 한데 묶어 종합적으로 출력 시퀀스에 대한 확률값을 계산하는 데 있다. 각각의 입력, 출력 정보는 표1에 정리했다.
표1 TRANSDUCERS

WFST를 음성 인식에 적용하는 과정을 도식적으로 나타낸 그림은 그림5와 그림6이다. 입력 음성을 MFCCs로 바꾸어 이를 학습이 완료된 히든 마코프 모델(Hidden Markov Model) + 가우시안 믹스처 모델(Gaussian Mixture Model)에 넣으면 상태 확률 벡터 시퀀스(HMM 상태 수 × MFCCs 프레임 개수)가 출력된다. 여기에서 비터비 알고리즘(Viterbi Algorithm), Word Lattice, 스택 디코딩(Stack Decoding) 등 기법을 적용한 결과가 HMM states(표1) 내지 Context dependent phones(그림10/그림11) 시퀀스이다. 이를 HMM Transducer에 넣으면 Context Independent phones(에 관련된 확률)가 출력된다.
그림5 CONCEPT (1)

Context Independent phones를 Context-dependency Transducer에 넣으면 음소(phone) 시퀀스(에 관련된 확률)가 출력된다. 음소 시퀀스를 Pronunciation lexicon Tranducer에 넣으면 단어(word) 시퀀스(에 관련된 확률)가 출력되고, 최종적으로 이를 Word-level Grammar Tranducer에 넣으면 교정된 형태의 새로운 단어 시퀀스(에 관련된 확률)를 얻을 수 있다.
그림6 CONCEPT (2)

우리는 네 가지 Transducer를 사용하고 있어 탐색해야할 경로가 엄청 많은 상황인데, 앞서 정의해두었던 연산을 요긴하게 써먹을 때가 왔다. 네 가지 Transducer를 차례대로 합성하되 겹치거나 불필요한 경로들을 미리 삭제해 두어 효율적인 경로 탐색/확률 계산이 가능하도록 한다. 수식2와 같다.
수식2 H ◦ C ◦ L ◦ G COMPOSITION
다음 항목에서는 각 Transducer와 합성 과정을 살펴본다.
4. Grammar Transducer
Grammar Transducer는 언어 모델(Language Model)이다. 그림7과 같다. 언어 모델은 단어 수준으로 학습됐으며 앞서 살펴봤듯이 입력과 출력 레이블이 동일하기 때문에 에지가 레이블/스코어 형태로 표시된 걸 확인할 수 있다.
그림7 GRAMMAR TRANSDUCER

5. Lexicon Transducer
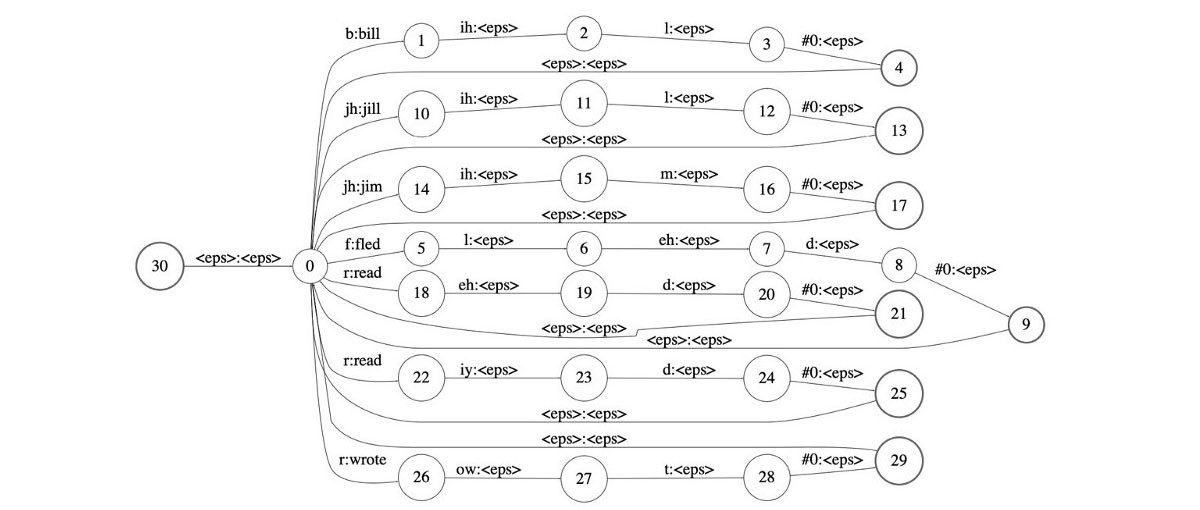
Lexicon Transducer는 발음 사전(pronouncitaion lexicon)이다. 그림8은 7개 단어에 관련된 발음 사전을 나타내고 있다. Lexicon Transducer는 입력이 음소 시퀀스(phones), 출력은 단어(word) 시퀀스이다. 이에 첫 번째 에지가 이후 에지 시퀀스의 디코딩 결과를 대변하고 있도록 하고 있다. 두 번째 이후의 전이(transition)는 출력이 모두 \(\epsilon\)(empty)임을 확인할 수 있다.
그림8 LEXICON TRANSDUCER
6. L ◦ G composition
수식2에서 확인할 수 있는 것처럼 가장 먼저 합성할 대상은 \(L\)과 \(G\)이다. 두 Transducer에 Determinization 연산을 우선 수행한 뒤 Minimization 연산을 적용한다. 그림9와 같다.
그림9 L ◦ G COMPOSITION
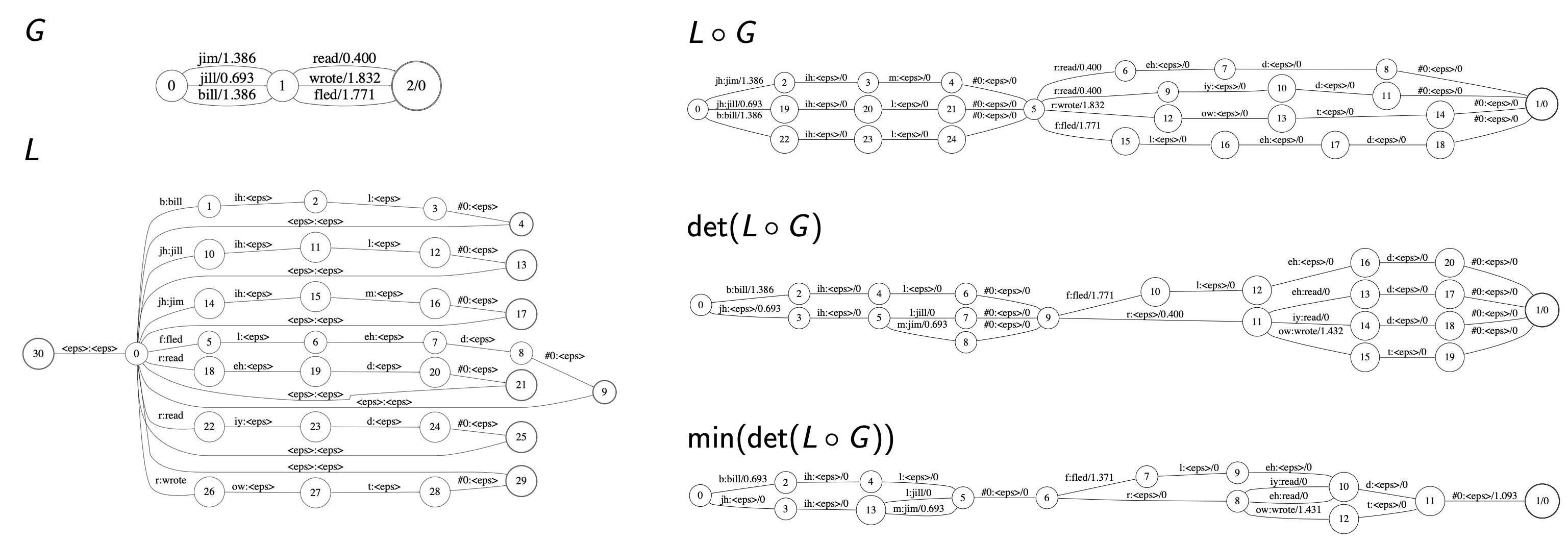
7. Context-dependent Transducer
Context-dependent Transducer는 Context-Dependent Phones(CD Phones)를 입력 받아 음소 혹은 Context-Independent Phones(CI Phones)라 불리는 시퀀스를 출력한다. 그림10과 같다. 그림10에서 에지는 입력 CD Phone : 출력 CI Phone / 왼쪽 컨텍스트 CD Phone_오른쪽 컨텍스트 CD Phone 형태로 표기되어 있다(스코어 내지는 확률값은 이해를 돕기 위해 생략).
그림10 CONTEXT-DEPENDENT TRANSDUCER

예컨대 첫 번째 에지인 x:x/e_y는 입력 CD Phone이 x이고 출력 CI Phone이 x라는 뜻이다. 단 입력이 되는 CD Phone(x)의 왼쪽(previous)엔 e(start 혹은 end), 오른쪽(next)엔 y가 등장했다는 전제 하에서이다. 따라서 첫 번째 에지의 입/출력은 각각 e-x-y, x가 된다. Context-dependent Transducer 입력(CD Phones)이 그림10과 같이 e-x-y x-y-x y-x-x x-x-y x-y-e일 경우 출력(CI Phones)은 x y x x y(에 관련된 확률)가 된다.
8. HMM Transducer
HMM Transducer는 HMM 상태(state) 시퀀스를 입력받아 Context-Dependent Phones(CD Phones)(에 관련된 확률)를 출력한다. 그림11과 같다. 그림11에서 에지는 HMM 상태 ID : CD Phone / 확률값 형태로 표시되어 있다.
그림11 HMM TRANSDUCER
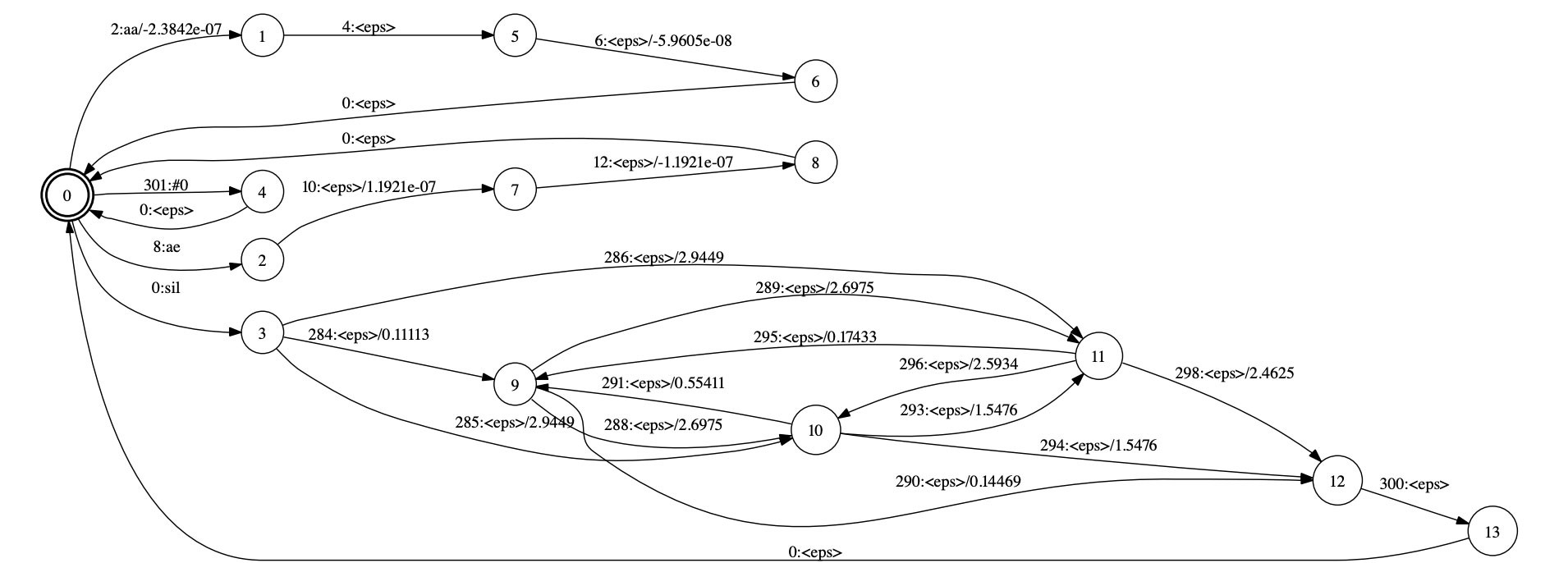
9. Decoding
이제 음성 입력을 받아 실제 인식 작업을 할 차례이다. 우선 음성을 MFCCs 피처로 바꾸고 이를 히든 마코프 모델 + 가우시안 믹스처 모델에 태운다. 그러면 상태 확률 벡터 시퀀스(HMM 상태 수 × MFCCs 프레임 개수)가 리턴된다.
이론적으로는 이것과 이미 만들어놓은 HCLG를 합성(composition)해 입력 음성에 대응하는 출력 단어 시퀀스의 최종 확률/스코어를 계산하는 것이 완벽할 결과를 낼 수 있을 것이다.
하지만 그래프 크기가 너무 크고 계산량이 많아 불가능에 가깝다. HMM 상태 확률 벡터 시퀀스에서 몇 개 후보(HMM 상태 시퀀스)를 찾아 이 후보 시퀀스 각각을 HCLG에 넣어 개별 후보 시퀀스에 대응하는 출력 단어 시퀀스의 확률/스코어를 계산하는 것이 효율적이다.
후보를 찾는 가장 간단한 방식으로는 HMM 상태 확률 벡터 시퀀스에서 각 시점(time), 상태(state)별로 베스트 경로 하나만 남기는 비터비 알고리즘(Viterbi Algorithm)이 있다. 1등 말고 \(n\)개 리스트를 탐색하는 Word Lattice도 대안이 될 수 있다. 끝까지 디코딩했을 때 기대되는 확률값을 고려하는 스택 디코딩(Stack Decoding) 혹은 \(A^{∗}\) 디코딩도 널리 쓰인다.