2. Viterbi Decoding
Info
비터비 알고리즘(Viterbi Algorithm)은 가장 널리 쓰이는 디코딩 방법 가운데 하나이다. 이 글에서는 히든 마코프 모델(Hidden Markov Model)을 예시로 비터비 디코딩 기법을 설명하도록 한다.
1. 개요
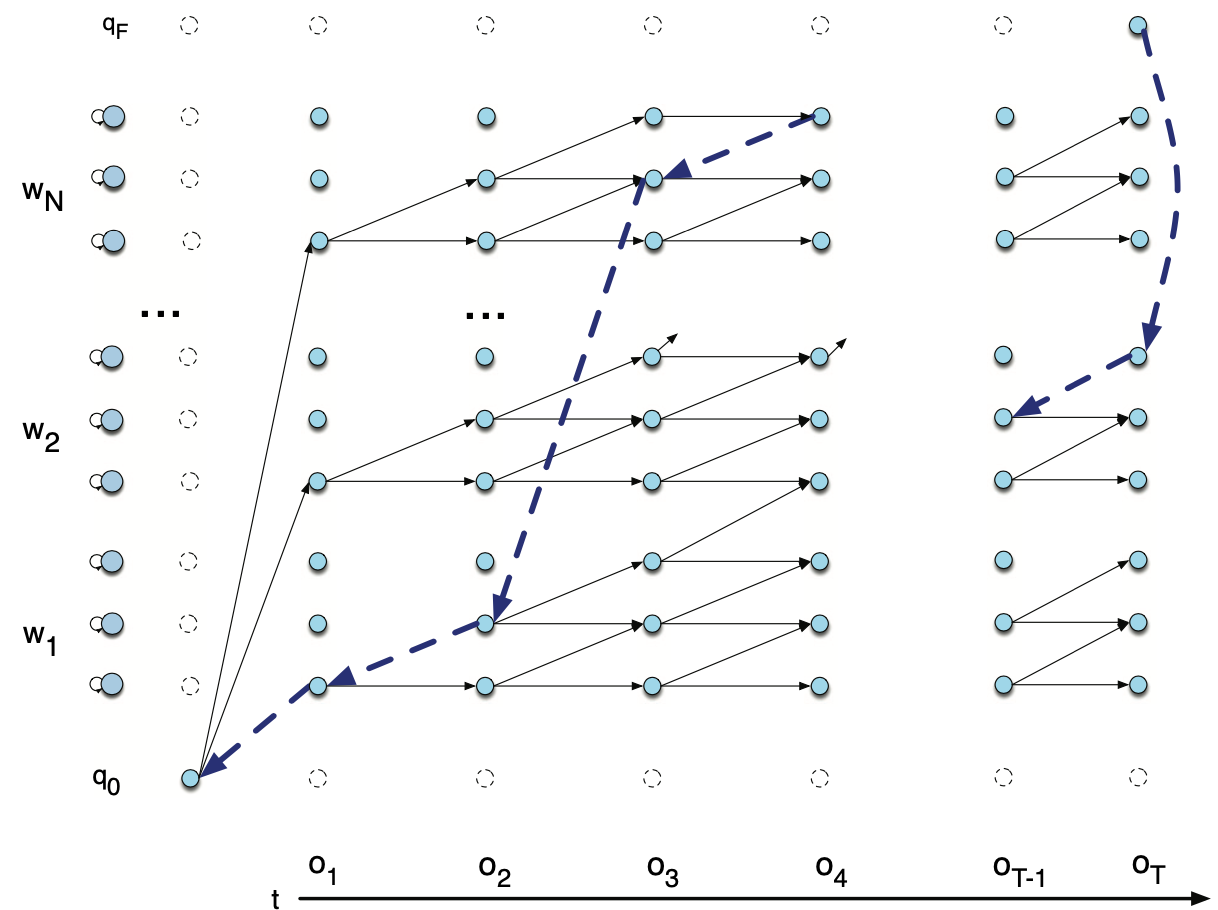
비터비 디코딩 과정을 개념적으로 만든 그림은 그림1과 같다. 현재 상태로 전이할 확률이 가장 큰 직전 스테이트를 모든 시점, 모든 상태에 대해 구한다.
그림1 VITERBI DECODING (1)
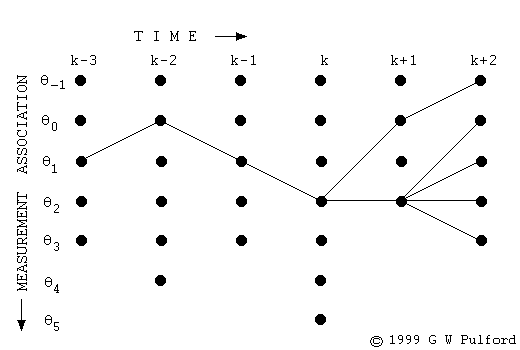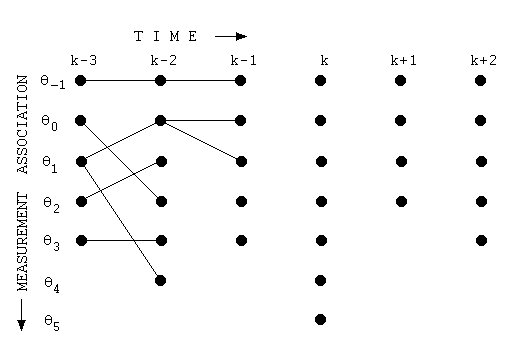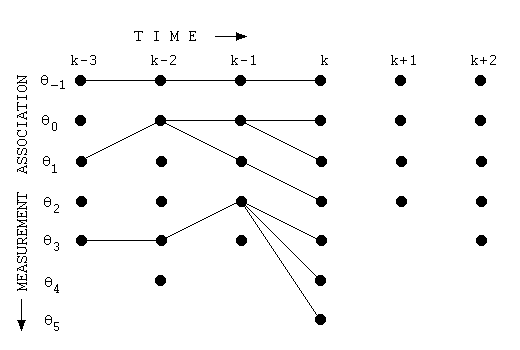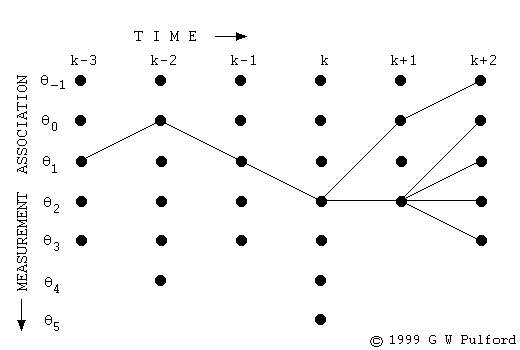
모든 시점, 모든 상태에 대해 구한 결과는 그림2와 같다(원래는 그물망처럼 촘촘하게 되어 있으나 경로가 끊어지지 않고 처음부터 끝까지 연결되어 있는 경로가 유효할 것이므로 그래프를 그린 사람이 이해를 돕기 위해 이들만 남겨 놓은 것 같다).
그림2 VITERBI DECODING (2)
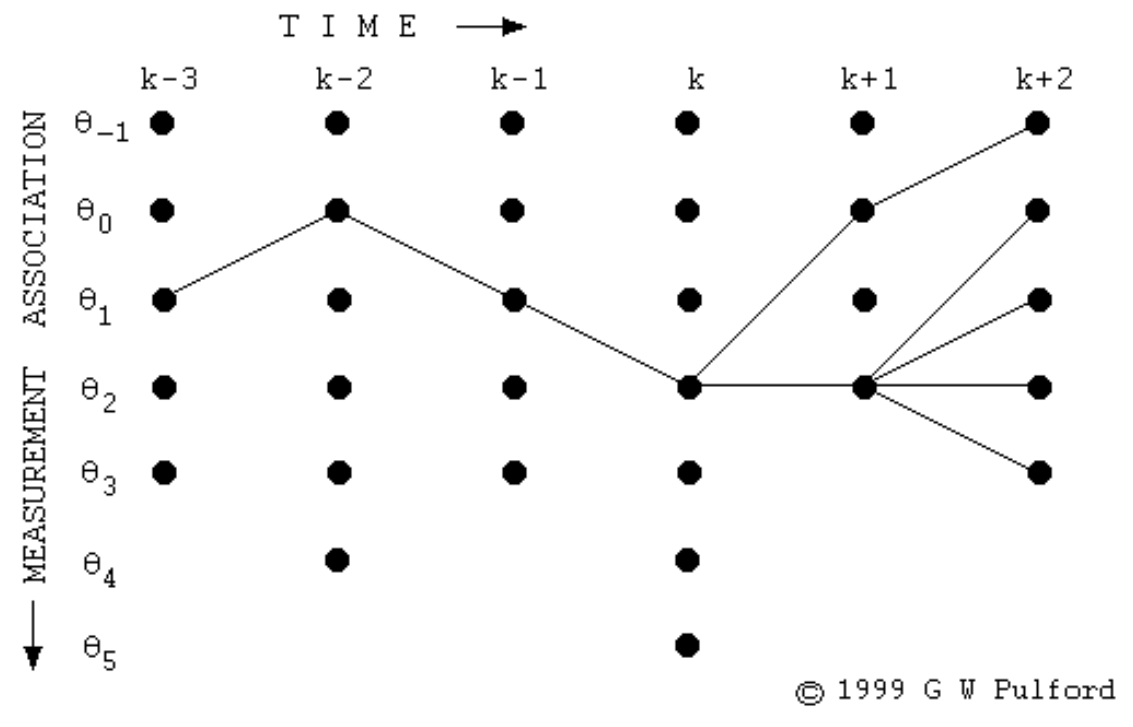
위 패스에서 만약 최대 확률을 내는 \(k+2\)번째 시점의 상태가 \(\theta_{0}\)라면 backtrace 방식으로 구한 최적 상태열은 다음과 같다.
- \(\left[\theta_{0}, \theta_{2}, \theta_{2}, \theta_{1}, \theta_{0}, \theta_{1}\right]\)
2. Forward Computation
비터비 알고리즘의 계산 대상인 비터비 확률(Viterbi Probability) \(v\)는 다음과 같이 정의된다. \(v_{t}(j)\)는 \(t\)번째 시점의 \(j\)번째 은닉상태의 비터비 확률을 가리킨다. 수식1과 같다.
수식1 VITERBI PROBABILITY
자세히 보면 Forward Algoritm에서 구하는 전방 확률 \(\alpha\)와 디코딩 과정에서 구하는 비터비 확률 \(v\)를 계산하는 과정이 거의 유사한 것을 확인할 수 있다. Forward Algorithm은 각 상태에서의 \(\alpha\)를 구하기 위해 가능한 모든 경우의 수를 고려해 그 확률들을 더해줬다면(sum), 디코딩은 그 확률들 가운데 최대값(max)에 관심이 있다.
이제 예를 들어본다. 학습이 완료된 히든 마코프 모델이 준비돼 있다. 전이 확률 \(A\)와 방출 확률 \(B\)의 추정을 모두 마쳤다는 이야기이다. 이제 \(P(\mathrm{O} \mid \mathrm{W})\), 즉 가능도(likelihood)를 계산해 본다. 예시에서는 상태(state)가 f(j=1), ay(j=2), v(j=3) 3가지뿐이고 self-loop이거나 left-to-right로 전이할 확률은 각각 0.5로 동일(uniform)하다. 방출확률 \(P\left(o_{t} \mid q_{j}\right)=b_{j}\left(o_{t}\right)\)는 표1의 \(B\)에 나열돼 있다.
그림3 FORWARD COMPUTATION

수식1에서 확인할 수 있듯 \(t\)번째 시점에 \(j\)번째 상태인 비터비 확률 \(v_{t}(j)\)는 전체 \(n\)개 직전 상태 각각에 해당하는 전방 확률들의 최댓값이다. 이를 그림3과 표1을 비교해서 보면 이렇다. \(t=1\), \(j=3\)일 때를 보자. \(v_{1}(3)\)은 0.8이 된다. 첫 번째 상태에서는 이전 상태가 존재하지 않기 때문에 첫 번째 상태의 비터비 확률 \(v_{1}(1)\)은 초기 상태 분포(initial state distribution)에서 뽑아 쓴다(0.8). 마찬가지로 구한 결과가 \(v_{1}(2)=0\), \(v_{1}(3)=0\)라고 해보자.
\(t=2\), \(j=1\)일 때를 보자. 최댓값 비교 대상이 되는 값들은 전체 3개 직전 상태 각각에 해당하는 전방 확률들의 최댓값이다. f(j=1)→f(j=1), ay(j=2)→f(j=1), v(j=3)→f(j=1) 가운데 최댓값을 취하면 된다(the most probale path).
그런데 음성 인식을 위한 히든 마코프 모델에서는 self-loop와 left-to-right 두 가지 경우로 전이(transition)에 대한 제약을 두고 있으므로 f(j=1)→f(j=1)만 고려 대상이 된다. f(j=1)→f(j=1)는 \(v_{1}(1) \times a_{11} \times b_{1}\left(o_{2}\right)\)가 되므로 \(0.8 \times 0.5 \times 0.8=0.32\)이다. 최댓값을 취해야 하는데 비교 대상 값이 하나뿐이므로 \(v_{2}(1)=0.32\)가 된다.
\(t=2\), \(j=2\)일 때를 보자. 최댓값 비교 대상이 되는 값들은 전체 3개 직전 상태 각각에 해당하는 전방 확률들의 최댓값이다. f(j=1)→ay(j=2), ay(j=2)→ay(j=2), v(j=3)→ay(j=2) 가운데 최댓값을 취하면 된다.
그런데 음성 인식을 위한 히든 마코프 모델에서는 self-loop와 left-to-right 두 가지 경우로 전이(transition)에 대한 제약을 두고 있으므로 f(j=1)→ay(j=2), ay(j=2)→ay(j=2)만 고려 대상이 된다.
f(j=1)→ay(j=2)는 \(v_{1}(1) \times a_{12} \times b_{2}\left(o_{2}\right)\)가 되므로 \(0.8 \times 0.5 \times 0.1=0.04\)입니다. ay(j=2)→ay(j=2)는 \(v_{1}(2) \times a_{22} \times b_{2}\left(o_{2}\right)\)이므로 \(0 \times 0.5 \times 0.1=0\)이다. 둘 중 최댓값을 취한 것이 비터비 확률이므로 \(v_{2}(2)=0.04\)이다.
표1 FORWARD COMPUTATION
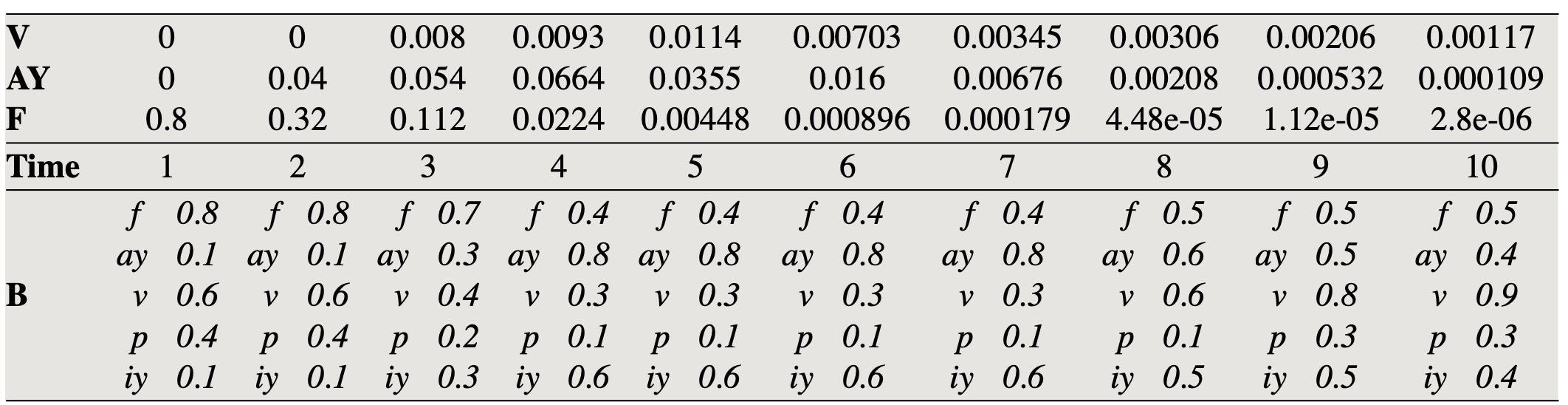
표1 상단의 각 상태에 해당하는 값들은 해당 시점/상태의 비터비 확률들이다.
3. Viterbi Search
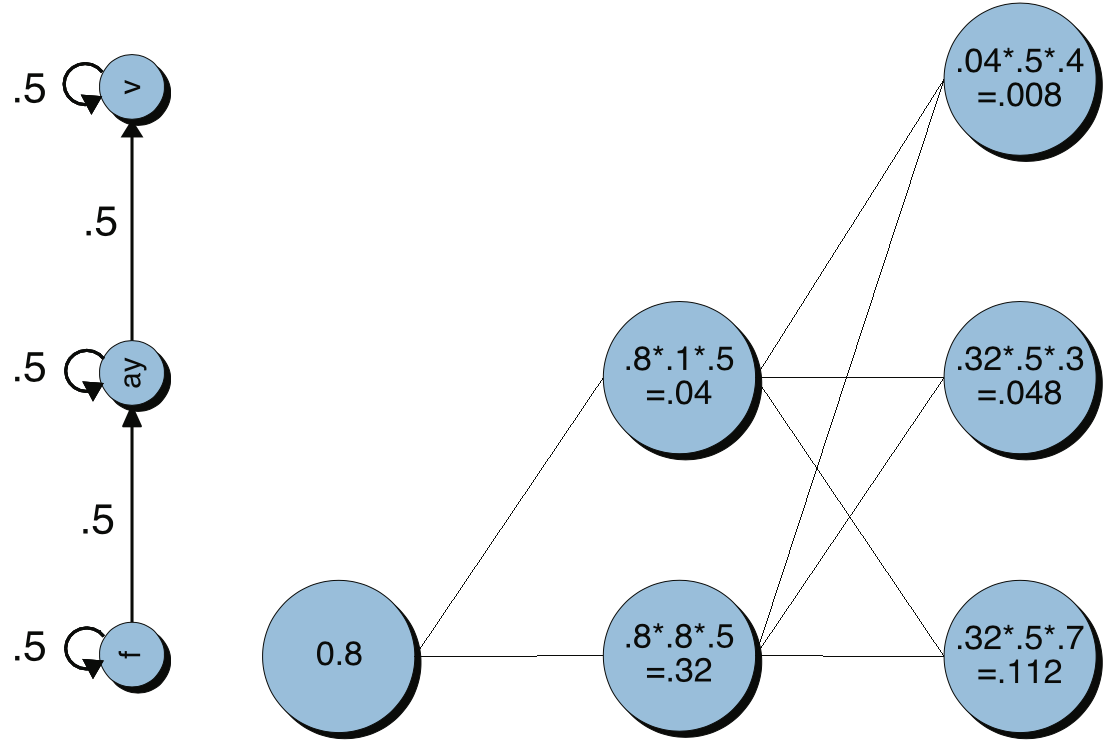
그림3은 Forward Computation으로부터 베스트 경로 하나만 남겨서 비터비 경로를 탐색하는 과정을 개념적으로 나타낸 것이다. 비터비 알고리즘을 찾은 후보 상태열의 경로들을 Viterbi Trellis라고 한다. 이후 최종적으로 베스트 경로를 찾아 역추적(backtrace)를 해야 한다. 역추적을 하는 이유는 매순간 최선의 선택이 전체 최적을 보장하지 못할 수도 있기 때문이다.
이해를 돕기 위해 비터비 확률을 모두 구한 결과 3번째 시점에서 끝이 났다고 해보자. 그림3은 각 시점/상태에서 비터비 알고리즘으로 찾은 베스트 경로들(trellis)만 남긴 결과이다. 이때 최종적인 비터비 확률은 \(\max (0.008,0.048,0.112)=0.112\)가 된다. 이 경로는 \(t=3\)일 때 상태가 f에 대응한다. 이를 역추적(backtrace)하면 [f, f, f]가 된다.
그림3 VITERBI TRELLIS
히든 마코프 모델의 디코딩을 바이그램 등 단어 수준으로 확대하더라도 비터비 알고리즘은 동일하게 적용한다. 그림4, 그림5는 바이그램(bigram) 모델의 Viterbi Trellis를 개념적으로 도식화한 것이다. \(t=4\)번째 시점의 비터비 경로가 기존 단어 내부에 있을 수도 다른 단어의 시작이 될 수도 있다. 이처럼 단어와 단어 사이를 넘나들며 비터비 경로가 만들어질 수 있다.
그림4 VITERBI TRELLIS (1)
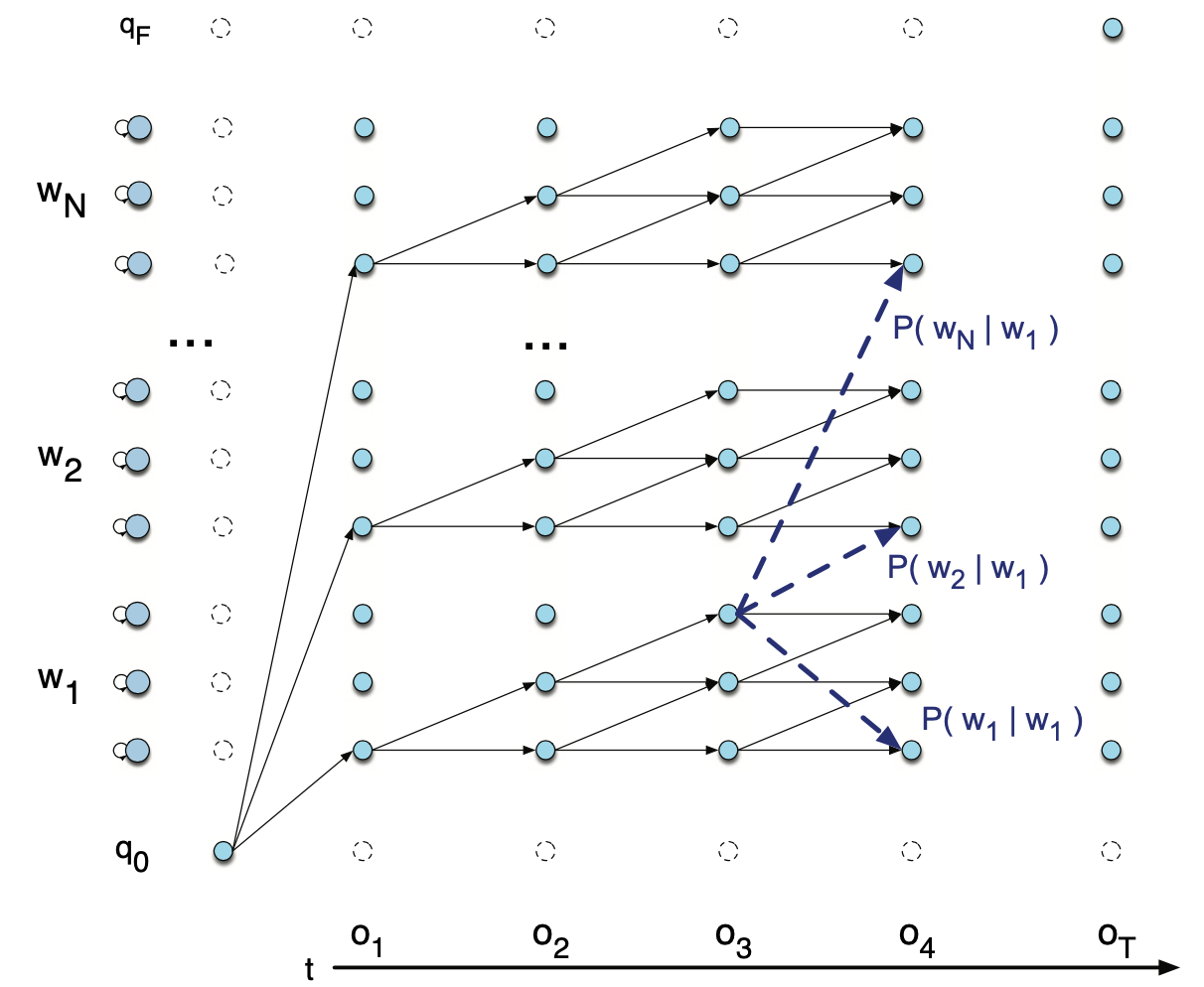
그림5 VITERBI TRELLIS (2)
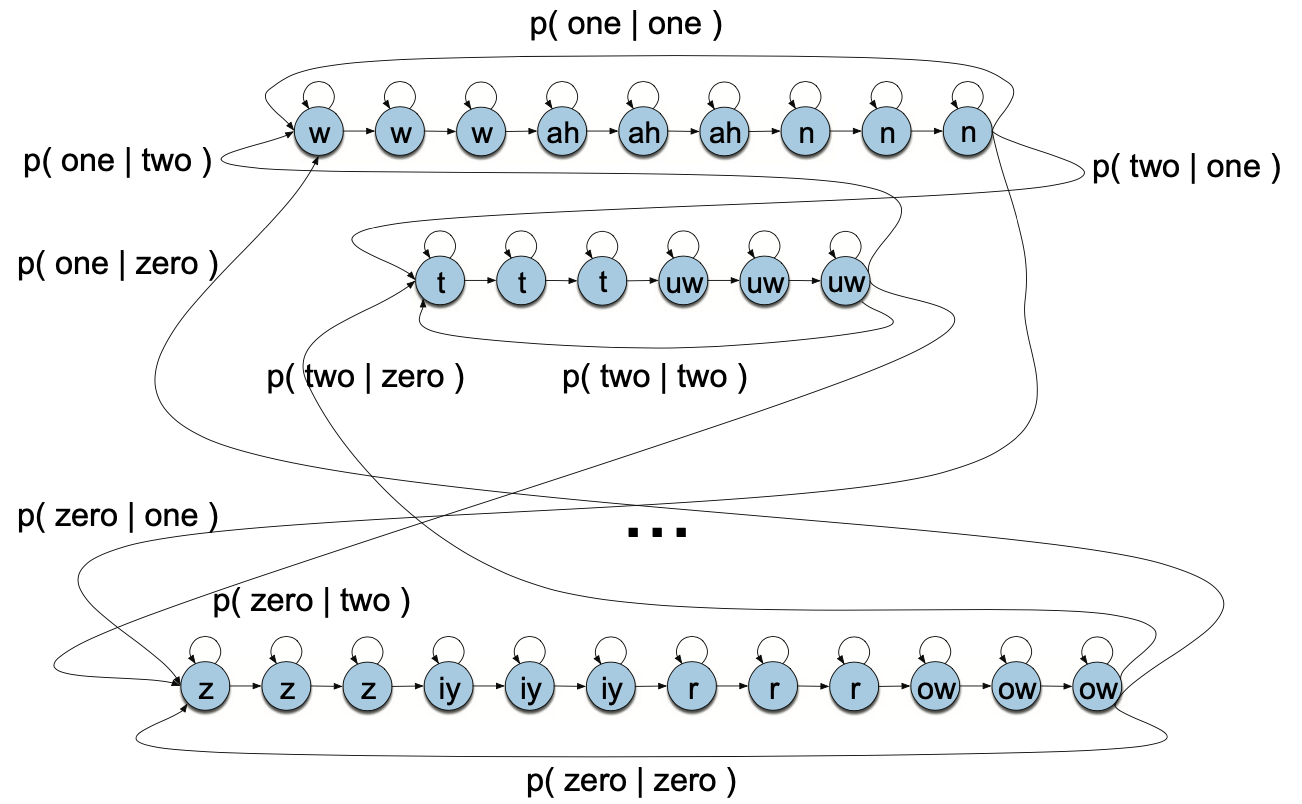
비터비 경로를 끝까지 찾고 최종적으로 가장 높은 확률값을 지닌 경로 하나를 선택한 뒤 해당 경로의 상태를 역추적(backtrace)해 디코딩 결과로 리턴한다.
그림5 VITERBI BACKTRACE