1. Decoding Strategy
Info
학습이 완료된 음성인식 모델을 가지고 입력 음성이 주어졌을 때 최적의 음소/단어 시퀀스를 디코딩하는 방법을 알아본다.
1. Acoustic + Language Model
대부분의 음성 인식 시스템(HMM+GMM 구조)에서는 디코딩 시 음향 모델(Acoustic Model)과 언어 모델(Language Model)을 함께 쓴다. 음향 모델을 가능도(likelihood) 함수로, 언어 모델을 사전확률(prior) 함수로 보고 베이지안 관점에서 모델링하는 것이다. 수식1과 같습니다.
수식1 음성인식 모델의 베이지안 모델링
그런데 음성은 대개 25ms 단위의 짧은 시간으로 잘라 프레임 피처로 변환해 모델에 입력하게 되는데, 이같이 자를 경우 10초짜리 음성이 400개 프레임이 모델에 입력되는 셈이다. HMM+GMM 구조에서는 각 프레임이 관측치(observation, \(o_{t}\))가 되고 해당 관측치의 상태(state, \(q_{j}\))를 추정하게 되는데, \(P\left(o_{t} \mid q_{j}\right)\)는 1보다 작고 시간 축(time step)을 따라 계속 곱해지기 때문에 프레임 개수가 많아질수록 수식1의 가능도(likelihood), 즉 \(P(O \mid W)\)가 과소추정(underestimate)될 가능성이 커진다.
이에 사전확률(prior)에 해당하는 언어 모델(language model) 스코어를 적당히 줄여서 프레임 길이에 따른 패널티가 없도록 없도록 구조를 바꿔준다. 이때 언어 모델의 지수로 들어가는 값을 Language Model Scaling Factor(LMSF)라고 한다. 언어 모델 스코어 역시 1 이하의 확률값이기 때문에 LMSF 값이 1 이상이면 언어 모델 스코어 값을 기존보다 줄일 수 있다. 대부분의 음성인식 시스템에서 LMSF 값으로 5~15 사이를 쓴다고 한다.
수식2 LANGUAGE MODEL SCALING FACTOR
언어 모델 스코어는 단어 개수가 많아질수록 작아진다. 예컨대 모든 단어 등장확률이 \(1 /|V|\)로 동일한 Uniform Language Model에서 \(N\)개 단어가 동시에 나타날 결합확률(joint probability)은 \(1 /|V|^{N}\)이 된다. 여기에서 \(V\)는 말뭉치 전체의 어휘(vocabulary) 수이다. 이에 단어 개수에 따른 언어 모델 스코어값의 패널티가 없도록 적당히 보정해주는 값을 곱해준다. 이 값을 Word Insertion Penalty(WIP)라고 한다. 수식3과 같다.
수식3 WORD INSERTION PENALTY
확률값에 로그를 취하면 곱셈이 덧셈으로 바뀌어 계산이 간결해진다. 언더플로(underflow) 문제도 막을 수 있다. 로그를 취한다고 해도 최댓값이 변하는 게 아니기 때문에 디코딩 결과에도 영향을 끼치지 않는다. 이에 수식4처럼 로그 확률로 변환해 디코딩을 수행하게 된다.
수식4 LOG PROBABILITY로 변환
2. Acoustic Model: Hidden Markov Model
기존 음성 인식 시스템의 음향 모델(Acoustic Model)은 히든 마코프 모델(Hidden Markov Model) 기반인 경우가 많다. 히든 마코프 모델에 가우시안 믹스처 모델(Gaussian Mixture Model)을 결합하거나, 히든 마코프 모델과 딥러닝/서포트 벡터 머신 등을 함께 쓰는 방식 등이 바로 그것이다. 그림1은 히든 마코프 모델 기반 음성 인식 모델의 디코딩 전반을 도식화한 그림이다.
그림1 HMM 기반 모델 디코딩
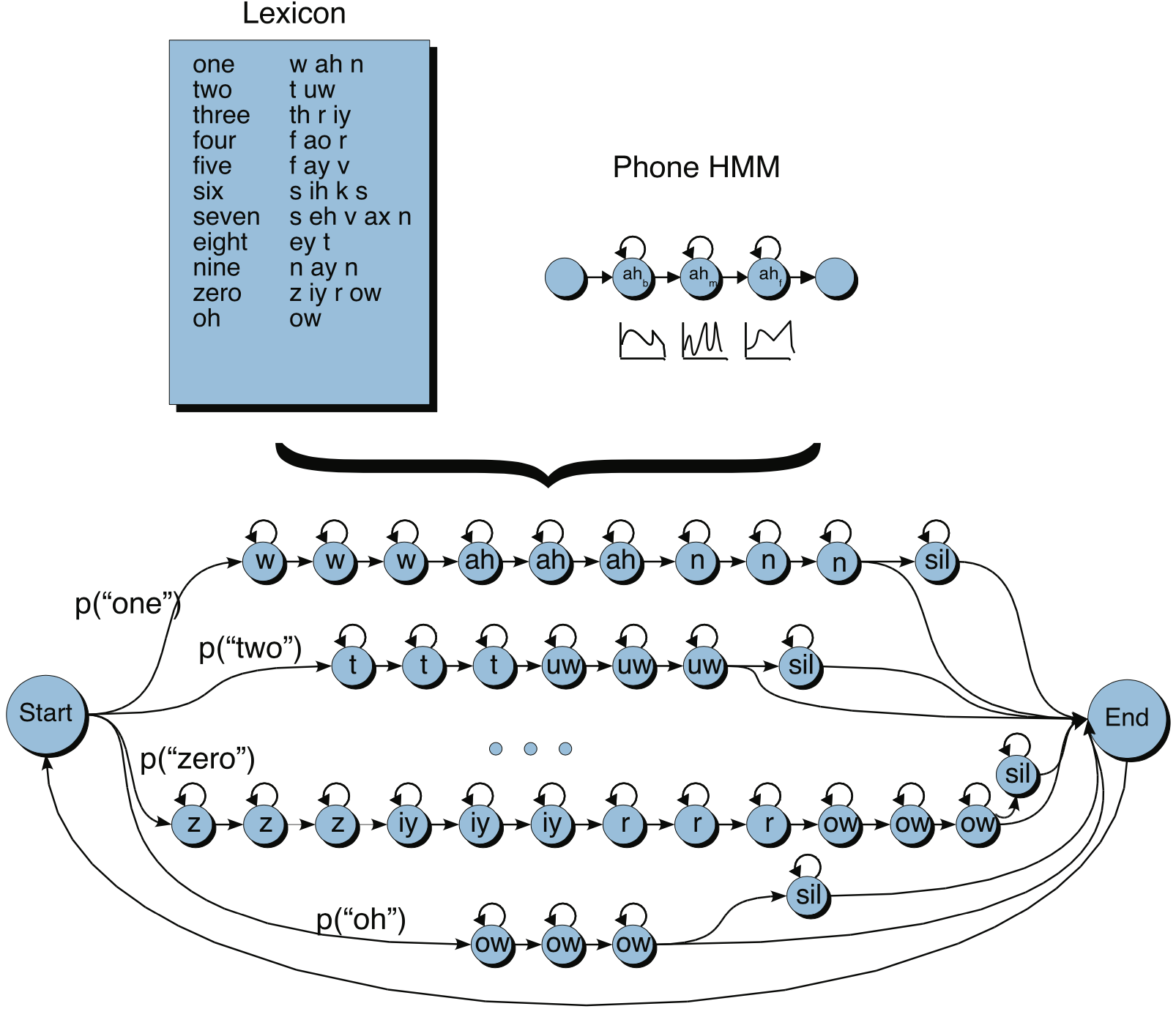
그림1에서 살펴볼 수 있듯 히든 마코프 모델 기반 음성 인식 모델의 각 상태(state)는 두 가지의 전이(transition)만 허용합니다: 셀프-루프(self-loop) 혹은 다음 상태로 전이. 이 2가지의 경우는 글자를 음소에 대응시켜주는 어휘사전(lexicon)을 바탕으로 한다. 이 어휘사전을 Grapheme To Phoneme(G2P)라고 한다.
히든 마코프 모델을 학습할 때 한 상태에서 다른 상태로 전이할 때 모든 가능성을 열어두는 것이 아니라 어휘사전을 바탕으로 상태 전이에 제약을 둔다는 이야기이다. 두 가지 이외의 전이 경로에 대해서는 그 값을 0으로 둬서 학습에서 제외한다. 한편 히든 마코프 모델 기반 음성 인식 모델은 상태를 음소(phone)보다 작은 단위의 subphone으로 모델링하고 있음을 확인할 수 있다.
그림1에서는 숫자 인식에 관련한 예시를 보여주고 있는데, 시작(start) 상태에서 어떤 단어(숫자)든지 전이할 수 있되, 한 단어에 해당하는 상태(subphone)가 시작되면 그 전이는 앞서 말했던 것처럼 어휘사전에 의해 제약이 가해진다. 단어 상태 시퀀스가 종료하면 끝(end) 상태에 다다르고 다시 어떤 단어든 전이할 수 있게 된다. 시작에서 끝 상태에 이르기까지 상태열(state sequence)의 길이는 유연하게 모델링되고 있음을 확인할 수 있다.
히든 마코프 모델 기반 음성 인식 모델은 입력 음성이 들어오면 어휘사전(\(W\))이 주어졌을 때 해당 음성(\(O\))이 나타날 가능도(likelihood), 즉 \(P(O \mid W)\)를 반환하게 된다. 이 가능도값은 이전 상태에서 다음 상태로 전이할 확률(transition probability)과 현재 상태에서 현재 관측치가 관측될 방출 확률(emission probability)의 곱(multiplication)으로 계산된다. 이때 방출 확률을 계산해주는 모듈이 가우시안 믹스처 모델(Guassian Mixture Model)이다. 이는 그림1의 Phone HMM에 개략적으로 도시되어 있다.
그림1의 히든 마코프 모델 기반 음향 모델(Acoustic Model)의 출력은 각 후보 상태열(state sequence)에 대한 가능도값, 즉 \(P(O \mid W)\)입니다. 이 값에 언어 모델 스코어까지 반영한 수식4를 최대화하는 단어 시퀀스 \(W\)가 히든 마코프 모델 기반 음성 인식 시스템의 최종적인 디코딩 결과가 된다.
3. End-to-End Model
최근에는 엔드투엔드(end-to-end)로 접근하려는 시도도 계속되고 있다. 지금까지 논의한 것과 별개로, 수식5와 같이 음성 시퀀스 \(O\)를 입력 받아 바로 단어 시퀀스 \(W\)를 예측하는 모델이다. 거의 대부분 딥러닝 기반 모델들이다. 이와 관련한 모델로는 Listen, Attend and Spell, Deep Speech 등이 있다. 이 시스템에서는 언어 모델 등의 도움 없이 바로 단어 시퀀스 \(W\)를 디코딩 결과로 리턴한다.
수식5 E2E MODEL
4. Evaluation
음성 인식 모델이 디코딩한 결과를 평가하는 것 역시 중요하다. 어떤 모델이 성능이 좋은지를 가늠해야 하기 때문인데, Word Error Rate(WER), Sentence Error Rate(SER), Matched-Pair Sentence Segment Word Error(MAPSSWE) test 등 3가지가 주로 쓰인다. 차례대로 살펴본다.
WER은 모델 예측 결과와 정답 사이의 단어 수준 편집거리(edit distance)를 수치화한 것이다. 수식5와 같다. 예측과 정답이 같을수록 그 값이 작아지고, 이 값이 작은 모델이 좋은 모델이라는 의미가 된다. SER은 전체 문장 개수 가운데 '단어 하나라도 틀린 문장 개수'의 비율을 나타내는 지표이다. 이 역시 값이 작을수록 좋다.
수식5 WORD ERROR RATE
수식6 SENTENCE ERROR RATE
SER은 단어가 하나라도 틀린 문장의 개수를 전체 문장 개수로 나눠주면 되기 때문에 이해에 무리가 없을 것 같고, WER을 좀 더 살펴보자. 예컨대 정답(REF)과 예측(HYP) 문장이 그림2처럼 되어 있다고 가정해보자. 각각의 편집거리를 구하면 다음과 같다.
그림2 WER 계산 예시

- Insertion(단어를 삽입해야 정답과 일치): 1건(PHONE)
- Substitution(단어를 대체해야 정답과 일치): 6건(TO>UM, FULLEST>IS, LOVE>LEFT, TO>THE, OF>PHONE, STORES>UPSTAIRS)
- Deletion(단어를 삭제해야 정답과 일치): 3건(GOT, IT, FORM)
이 결과를 수식5에 따라 계산하면 WER은 \(100×(1+6+3)/13=76.9\)가 된다.
MAPSSWE 테스트는 두 개의 음성 인식 시스템의 성능 차이를 통계적으로 유의한 차이가 있는지 검정해보는 것이다. 어떻게 평가하는지 그림3을 예시로 설명해 본다. 우선 모델 예측 결과를 세그먼트(segment)로 나눈다. 보통의 음성 인식 시스템에서는 트라이그램(trigram) 언어 모델을 사용하므로, 두 모델이 모두 정답을 맞춘 어구(phrase) 앞뒤로 세그먼트 경계를 나눈다.
그림3 MAPSSWE 계산 예시

그림3에서 I 영역에서 모델 A는 2개(Substitution 1건, Insertion 1건) 틀렸다. 모델 B는 모두 맞췄다. II 영역에서는 모델 A가 0건, B가 1건(Insertion) 틀렸다. III 영역에서는 A가 1건(Substitution), B가 2건(Substitution) 틀렸다. IV 영역에서는 A가 1건(Deletion), B가 0건 들렸다.
통계 검정을 위해 확률변수(random variable) \(Z\)를 \(N_{A}^{i}-N_{B}^{i}\)로 정의한다. \(i\)번째 세그먼트에서 모델 A가 틀린 개수, \(N_{B}^{i}\)는 같은 영역에서 모델 B가 틀린 개수를 가리킨다. 그림3의 예시에서는 \(Z\)의 값(value)이 2, -1, -1, 1이 된다. 만약 두 모델이 성능 차이가 없다면 \(\mu_{Z}\)가 0일 것이다(\(H_{0}: \mu_{Z}=0\)). \(Z\)의 표본평균과 표본분산은 수식7과 같다.
수식7 \(Z\)의 표본평균과 표본분산
이를 바탕으로 한 새로운 확률변수 \(W\)를 \(\hat{\mu}_{Z} /(\hat{\sigma} / \sqrt{n})\)으로 둔다면 표본의 개수 \(n\)이 50 이상으로 충분히 클 때 \(W\)는 근사적으로 정규분포를 따른다고 한다. 이에 \(2 \times P(Z \geq|W=w|) \leq 0.05\)인 경우 귀무가설 \(H_{0}\)(모델 A와 B의 성능이 동일하다)를 기각(reject)하게 된다(two-tailed test).