5. Connectionist Temporal Classification
Info
입력 음성 프레임 시퀀스와 타겟 단어/음소 시퀀스 간에 명시적인 얼라인먼트(alignment) 정보 없이도 음성 인식 모델을 학습할 수 있는 기법인 Connectionist Temporal Classification(CTC)를 살펴본다.
1. Motivation
음성 인식 모델을 학습하려면 음성(피처) 프레임(그림1에서 첫 번째 줄) 각각에 레이블 정보가 있어야 한다. 음성 프레임 각각이 어떤 음소인지 정답이 주어져 있어야 한다는 이야기이다. 그런데 MFCC 같은 음성 피처는 짧은 시간 단위(대개 25ms)로 잘게 쪼개서 만들게 되는데, 음성 프레임 각각에 레이블(음소)을 달아줘야 하기 때문에 다량의 레이블링을 해야 하고(고비용) 인간은 이같이 짧은 구간의 음성을 분간하기 어려워 레이블링 정확도가 떨어진다.
Connectionist Temporal Classification(CTC)는 입력 음성 프레임 시퀀스와 타겟 단어/음소 시퀀스 간에 명시적인 얼라인먼트(alignment) 정보 없이도 음성 인식 모델을 학습할 수 있도록 고안됐다. 다시 말해 입력 프레임 각각에 레이블을 달아놓지 않아도 음성 인식 모델을 학습할 수 있다는 것이다. 물론 음성 인식 태스크가 아니어도 소스에서 타겟으로 변환하는 모든 시퀀스 분류 과제에 CTC를 적용할 수 있다(예: 손글씨 실시간 인식, 이미지 프레임 시퀀스를 단어 시퀀스로 변환).
그림1 CTC INPUT

CTC 기법은 시퀀스 분류를 위한 딥러닝 모델 맨 마지막에 손실(loss) 및 그래디언트 계산 레이어로 구현이 된다. CTC 레이어의 입력은 출력 확률 벡터 시퀀스(그림1 하단)이다. 그림1에서는 Recurrent Neural Network가 CTC 입력에 쓰이는 확률 벡터 시퀀스를 만드는 데 쓰였다. 하지만 트랜스포머(Transformer) 등 시퀀스 출력을 가지는 어떤 아키텍처든 CTC 기법을 적용할 수 있다.
그림1에서 확인할 수 있듯 CTC 레이어가 입력 받는 확률 벡터의 차원수는 레이블 수 + 1이다. 1이 추가된 이유는 \(\mathcal{E}\), 즉 blank가 포함되어 있기 때문이다. 예컨대 한국어 전체 음소 수가 42개라면 CTC에 들어가는 확률 벡터의 차원 수는 43차원이 된다. CTC 레이어에서는 그림1 하단과 같은 확률 벡터 시퀀스를 입력 받아 손실을 계산하고 그에 따른 그래디언트를 계산해 준다. 이후 여느 딥러닝 모델을 학습하는 것처럼 역전파(backpropagation)로 모델을 업데이트하면 된다.
그림2는 CTC 기법으로 학습한 모델을 예측하는 과정을 도식화한 것이다. 먼저 입력 프레임별 예측 결과를 디코딩(decoding)한다. 이후 반복된 음소와 blank를 제거하는 등의 후처리를 해서 최종 결과물을 산출한다.
그림2 CTC PREDICTION

2. All Possible Paths
CTC 기법에서는 레이블과 레이블 사이의 전이(transition)를 다음 세 가지의 경우로만 한정한다.
1] selp-loop: 자기 자신을 반복한다.
2] left-to-right: non-blank 레이블을 순방향으로 하나씩 전이한다. 역방향은 허용하지 않는다. non-blank를 두 개 이상 건너뛰는 것 역시 허용이 안 된다.
3] blank 관련: blank에서 non-blank, non-blank에서 blank로의 전이를 허용한다.
CTC 입력 확률 벡터 시퀀스가 8개이고 정답 레이블 시퀀스 \(\mathbf{l}\)이 h,e,l,l,o일 때 위와 같은 제약을 바탕으로 가능한 모든 경로(path)를 상정해본 결과는 그림3과 같다. \(\mathbf{l}\)의 시작과 끝, 레이블 사이사이에 blank를 추가한 시퀀스를 \(\mathbf{l}^{\prime }\)이라고 합니다(이제부터는 blank를 -로 표기한다). 따라서 \(\mathbf{l}^{\prime }\)의 길이는 \(2 \times|1|+1\)이 된다. 그림3 가로축은 이해를 돕기 위해 \(\mathbf{l}^{\prime }\)을 순서대로 그린 것에 해당하고, 사실은 같은 시점에 중복된 레이블에 해당하는 \(y\) 확률값은 동일하며 \(\mathbf{l}^{\prime }\) 말고도 나머지 레이블 역시 있다고 상상하면 좋을 것 같다. 그림3에서 녹색 실선에 대응하는 것은 hello---, 검정색 실선에 대응하는 것은 ---hello이다.
그림3 ALL POSSIBLE PATHS
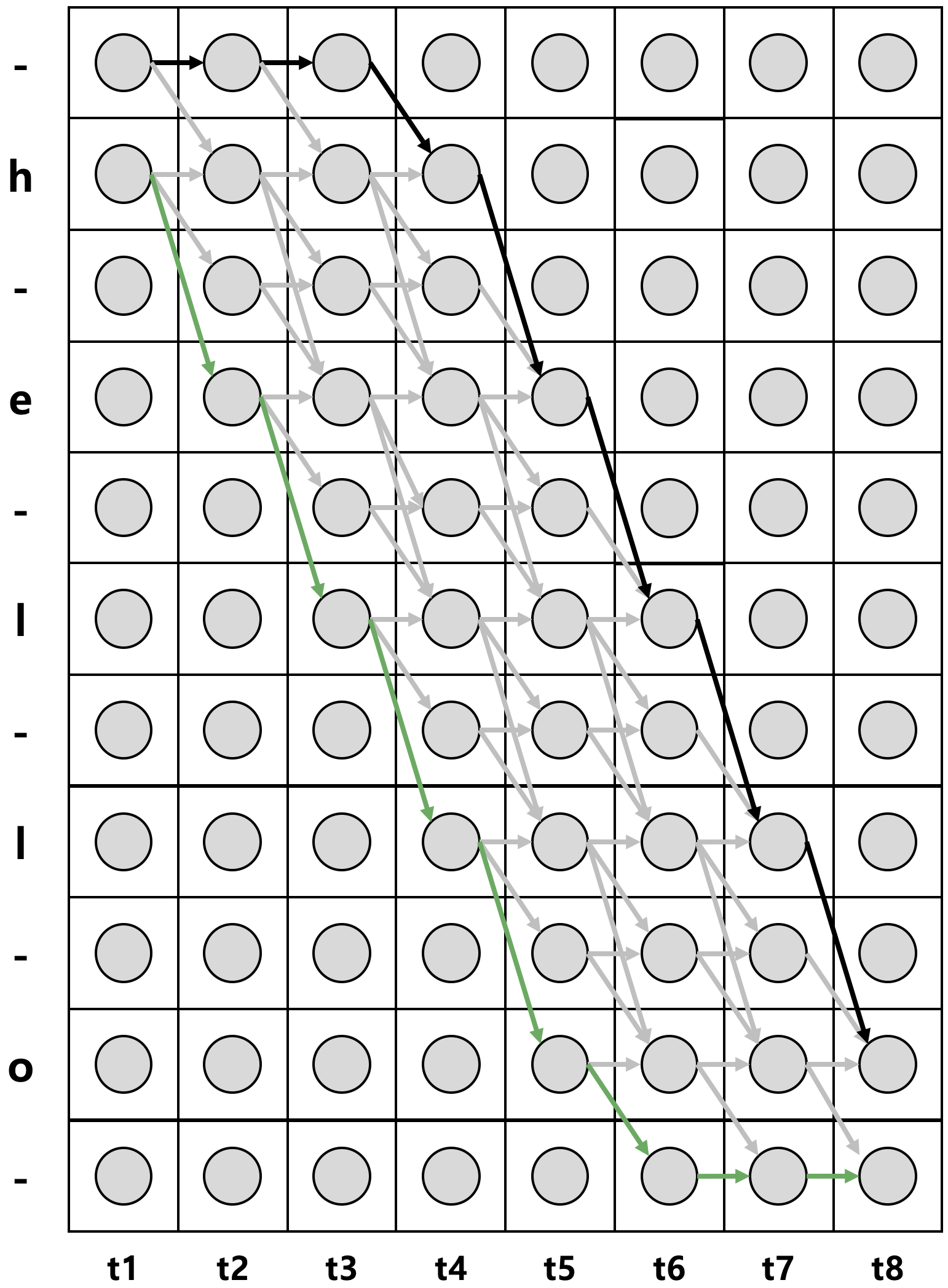
그림4는 그림3에서 해당 언어 조음 규칙상 절대로 발음될 수 없는 일부 경로들을 제거해 컴팩트하게 다시 그린 것이다. 녹색 실선에 대응하는 것은 hel-lo--, 검정색 실선에 대응하는 것은 --hel-lo이다. 앞으로는 그림4를 기준으로 손실 및 그래디언트를 계산해 본다.
그림4 ALL POSSIBLE PATHS

그림4에서 가로축은 시간(time, 인덱스는 \(t\)로 표기)을 나타낸다. 세로축은 상태(state, 음소, 인덱스는 \(s\)로 표기)이다. 각 세로 열은 각 시점에 해당하는 확률 벡터이다. 동그라미는 개별 확률값을 의미한다. 예컨대 그림4 2번째 행, 2번째 열의 동그라미는 \(y_{h}^{2}\), 즉 \(t=2\) 시점에 상태가 \(h\)일 확률을 가리킨다. 상태를 인덱스(index)로 표현하면 2번째 행, 2번째 열의 동그라미는 \(y_{2}^{2}\), 3번째 행, 2번째 열의 동그라미는 \(y_{3}^{2}\)로 표기할 수도 있다. 각각 \(t=2\) 시점에 h가 나타날 확률, \(t=2\) 시점에 -가 나타날 확률을 뜻한다.
\(\pi\)란 그림4의 좌측 상단에서 출발해 우측 하단에 도착하는 많은 경로 가운데 하나를 가리킨다. \(\pi\)는 -으로 시작하거나 레이블 시퀀스 \(\mathbf{l}\)의 첫 번째 레이블로 시작할 수 있다. 아울러 \(\pi\)는 \(\mathbf{l}\)의 마지막 레이블로 끝나거나 -로 종료할 수 있다. 그림4로 예로 들면 검정색 실선이 \(\pi\)가 될 수 있고, 녹색 실선이 될 수도 있다. 만일 검정색 실선이 \(\pi\)라고 가정하면 \(\pi\)는 --hel-lo이 된다. \(\pi_{t}=3\)는 h, 즉 \(s=2\)가 된다.
CTC 기법에서는 각 상태가 조건부 독립(conditional independence)라고 가정한다. 다시 말해 입력 음성 피처 시퀀스 \(\mathbf{x}\)에만 \(y\) 확률값들이 변할 뿐, 이전/이후 상태가 어떻든 그 값이 변하지 않는다고 가정하는 것이다. 이렇게 가정하면 \(\mathbf{x}\)가 주어졌을 때 \(\pi\)가 나타날 확률을 수식1처럼 \(y_{\pi_{t}}^{t}\)의 곱으로 나타낼 수 있다.
그림5 CONDITIONAL INDEPENDENCE

수식1 PATH PROBABILITY
입력 음성 피처 시퀀스 \(\mathbf{x}\)가 주어졌을 때 정답 레이블 시퀀스 \(\mathbf{l}\)이 나타날 확률은 상정 가능한 모든 경로(\(\pi\))들의 확률, 즉 \(p(\pi \mid \mathbf{x})\)를 더해주면 된다. 이를 식으로 나타낸 결과는 수식2와 같다. 여기에서 \(\mathcal{B}\)에 주목할 필요가 있다. \(\mathcal{B}\)는 blank와 중복된 레이블을 제거하는 함수이다. 예컨대 \(\mathcal{B}({ hheell-lo- })=\mathcal{B}({ hello })\)이다. \(\mathcal{B}^{-1}(\mathbf{l})\)은 blank와 중복된 레이블을 제거해서 \(\mathbf{l}\)이 될 수 있는 모든 가능한 경로들의 집합을 의미한다. 그림4에서 회색 화살표 위를 지나는 모든 경로들이 \(\mathcal{B}^{-1}(\mathbf{l})\)에 해당한다.
수식2 ALL PATHS PROBABILITY
3. Forward Computation
수식1과 수식2에서 살펴보았듯이 \(p(\mathbf{l} \mid \mathbf{x})\)를 구하려면 상정 가능한 모든 경로들에 대해 모든 시점, 상태에 대한 확률을 계산해야 한다. 시퀀스 길이가 길어지거나 상태(음소) 개수가 많아지면 계산량이 폭증하는 구조인데, CTC에서도 이를 방지하기 위해 히든 마코프 모델(Hidden Markov Model)과 같이 Forward/Backward Algorithm을 사용한다. 그림6의 예를 들어 설명해 본다.
그림6의 파란색 칸의 전방 확률(Forward Probability)를 구해보자. 이는 \(\alpha_{3}(4)\)로 표기할 수 있는데, \(t=1\) 시점 \(s=1\)의 상태(-) 혹은 \(t=1\) 시점 \(s=2\)의 상태(h)에서 시작해 시간 순으로 전이가 이루어져 \(t=3\) 시점에 \(s=4\)의 상태(e)가 나타날 확률을 가리킨다. \(t=3\) 시점에 e가 나타나려면 모든 경로 가운데 4가지 경우의 수만 존재한다. -he, hhe, h-e, hee가 바로 그것인데, 해당 경로들은 그림6에서 파란색 화살표로 표시되어 있다.
그림6 FORWARD COMPUTATION EXAMPLE

-he가 나타날 확률은 어떻게 구할까? 우리는 이미 조건부 독립을 가정했으므로 각 시점에 해당 상태가 나타날 확률을 단순히 곱셈을 해주면 된다. 마찬가지로 나머지 3개 경로, 즉 hhe, h-e, hee에 대해서도 같은 방식으로 구한다. 이를 모두 더한 결과가 \(\alpha_{3}(4)\)이 될 것이다. 수식4와 같다.
수식4 FORWARD COMPUTATION EXAMPLE
전방 확률 계산을 일반화한 식은 수식5이다. 전방 확률은 \(1:t\) 시점에 걸쳐 레이블 시퀀스가 \(1:s\)가 나타날 확률을 의미한다. 수식5를 이해할 때 핵심은 계산 대상 경로인 \(\it\)\(\pi\)(수식4의 예시에서는 -he, hhe, h-e, hee)를 찾는 일이 퇼텐데, 계산 대상이 되는 \(\pi\)의 조건은 다음과 같다.
1] \(1:t\) 시점까지의 \(\pi\)에서 blank와 중복 레이블을 제거한 결과가 \(1:s\)까지의 정답 레이블 시퀀스와 일치해야 한다. 수식4의 예시를 보면 blank와 중복 레이블을 제거한 결과가 he인 모든 경로(he, hhe, h-e, hee)를 의미한다.
2] \(\pi\)는 개별 요소가 상태(음소)인 시퀀스인데, 요소 각각이 \(N\)개의 범주를 가지며 시퀀스 전체 길이는 \(T\)이다. CTC는 입력 음소 시퀀스(그 길이는 \(T\)) 각각에 대해 음소 레이블을 부여(alignment)해주는 역할을 수행한다는 사실과 연관지어 이해해보면 좋을 것 같다.
수식5 FORWARD PROBABILITY
수식5처럼 계산할 경우 계산량이 너무 많아진다. 겹치는 부분은 저장해뒀다가 다시 써먹으면 효율적일 것이다. 이같은 알고리즘을 다이내믹 프로그래밍(Dynamic Programming)이라고 한다. 수식4에서 겹치는 부분을 찾아 다시 쓰면 수식6과 같다. \(\alpha_{2}(2)\), \(\alpha_{2}(3)\), \(\alpha_{2}(4)\)는 그림6에서 녹색으로 칠한 칸을 나타낸다. 전방 확률 계산에 다이내믹 프로그래밍을 적용한 기법을 Forward Algorithm이라고 한다. Forward Algorithm을 적용하게 되면 \(t\)시점에 전방 확률을 구할 때 이전 시점(\(t−1\))에 이미 계산해 놓은 전방 확률 값들을 재사용할 수 있게 된다.
수식6 DYNAMIC PROGRAMMING EXAMPLE
Forward Algorithm을 일반화해서 적용할 때 고려해야 하는 경우가 두 가지 있다. 계산 대상 현재 상태가 blank이거나, 현재 상태와 그 직직전 상태가 일치할 경우(CASE1)와 그 이외 케이스(CASE2)를 구분해야 한다는 점이다. 앞서 Forward Algorithm 계산 예시로 든 수식6의 경우 CASE2에 해당한다.
그림7 CASE 1

그림8 CASE 2

이상의 논의를 종합하여 전방 확률 계산을 도식적으로 나타낸 그림은 그림9와 같다. 경로는 blank 혹은 레이블 시퀀스 \(\mathbf{l}^{\prime }\)의 첫 번째 요소로 시작한다. \(\mathbf{l}^{\prime }\)의 마지막 요소 혹은 blank로 끝을 맺는다. 경로 중간에 있는 상태들의 전방 확률 계산은 CASE1 혹은 CASE2에만 해당하므로 해당 케이스에 맞춰 계산해 준다. 이를 식으로 표현하면 수식7과 같다.
그림9 FORWARD FLOW

수식7 FORWARD ALGORITHM
4. Backward Computation
이번에는 그림10의 오렌지색 칸의 후방 확률(Backward Probability)을 계산해 보자. 이는 \(\beta_{6}(9)\)로 표기할 수 있는데, \(t=8\) 시점 \(s=11\)의 상태(-) 혹은 \(t=8\) 시점 \(s=10\)의 상태(o)에서 시작해 시간의 역순으로 전이가 이루어져 \(t=6\) 시점에 \(s=9\)의 상태(-)가 나타날 확률을 가리킨다. 다시 말해 우측 하단 끝 지점에서 시작해 \(t=6\) 시점에 -가 나타나려면 모든 경로 가운데 2가지 경우의 수만 존재한다는 이야기이다. 이해를 돕기 위해 시간 순으로 정렬해 해당 경로들을 나타내면 --o, -oo, -o-가 바로 그것이다. 이 경로들은 그림10에서 붉은색 화살표로 표시되어 있습니다. 그림10의 \(\beta_{6}(9)\)를 계산한 결과는 수식8과 같다.
그림10 BACKWARD COMPUTATION EXAMPLE

수식8 BACKWARD COMPUTATION EXAMPLE
후방 확률 계산을 일반화한 식은 수식9이다. 입력 음성 시퀀스의 길이가 \(T\), 타겟 레이블 시퀀스가 \(\mathbf{l}\)이라고 할 때 \(t\) 시점의 후방 확률은 \(t:T\) 시점에 걸쳐 레이블 시퀀스가 \(s:|\mathbf{1}|\)일 확률을 의미한다. 계산 대상이 되는 \(\pi\)의 조건은 다음과 같다.
1] \(t:T\) 시점까지의 \(\pi\)에서 blank와 중복 레이블을 제거한 결과가 \(s:|\mathbf{1}|\)까지의 정답 레이블 시퀀스와 일치해야 한다. 수식8의 예시를 보면 blank와 중복 레이블을 제거한 결과가 o인 모든 경로(-o, oo, o-)를 의미한다.
2] \(\pi\)는 개별 요소가 상태(음소)인 시퀀스인데, 요소 각각이 \(N\)개의 범주를 가지며 시퀀스 전체 길이는 \(T\)이다.
수식9 BACKWARD PROBABILITY
전방 확률 계산 때와 마찬가지로 수식8처럼 계산하는 것 대신 다이내믹 프로그래밍을 적용하면 계산량이 줄어든다. 수식8에서 겹치는 부분을 찾아 다시 쓰면 수식10과 같다. 후방 확률은 전방 확률의 역이므로, Backward Algorithm을 적용하게 되면 \(t\) 시점 후방 확률을 구할 때 다음 시점(\(t+1\))에 이미 계산해 놓은 후방 확률 값들을 재사용할 수 있게 된다. 이같이 후방 확률 계산에 다이내믹 프로그래밍을 적용한 기법을 Backward Algorithm이라고 한다. \(\beta_{7}(9)\), \(\beta_{7}(10)\)은 그림10에서 노란색으로 칠한 칸을 나타낸다.
수식10 DYNAMIC PROGRAMMING EXAMPLE
Backward Algorithm 역시 Forward Algorithm 때처럼 CASE1과 CASE2로 나누어 계산한다. 전방 확률 계산과 그 방향이 달라졌을 뿐 본질적인 계산 방식은 동일하다. 그림10의 예제는 CASE1에 해당한다. Backward Algorithm을 일반화한 식은 수식11과 같다.
수식11 BACKWARD ALGORITHM
5. Complete Path Calculation
이번엔 특정 시점, 특정 상태를 지나는 경로에 대한 등장 확률을 구해본다. 이는 앞서 구한 전방 확률과 후방 확률로 간단히 계산할 수 있다. 그림11에서 파란색으로 칠한 칸을 보자. \(t=3\) 시점에 상태가 h(\(s=2\))인 모든 경로에 대한 확률을 구해보자는 것이다. 해당 경로는 --hel-lo, -hhel-lo, hhhel-lo 3가지가 존재한다.
그림11 COMPLETE PATH CALCULATION EXAMPLE

--hel-lo, -hhel-lo, hhhel-lo 3가지 경로에 대한 확률은 물론 모든 시점, 상태에 대해 일일이 곱셈을 하여서 구할 수 있다. 하지만 지금까지 설명했던 전방 확률과 후방 확률을 활용하면 좀 더 효율적으로 구할 수 있다. 파란색 칸에 대한 전방 확률과 후방 확률은 각각 수식12, 수식13과 같다.
수식12 FORWARD PROBABILITY EXAMPLE
수식13 BACKWARD PROBABILITY EXAMPLE
수식14는 수식12의 전방 확률과 수식13의 후방 확률을 곱한 것이다. 식을 자세히 보시면 전방 확률과 후방 확률의 곱은 우리가 구하고자 하는 --hel-lo, -hhel-lo, hhhel-lo 3가지 경로에 대한 확률을 더한 값에 \(y_{h}^{3}\)이 곱해진 형태임을 확인할 수 있다. 수식11의 양변을 \(y_{h}^{3}\)으로 나눠주면 우리가 구하고자 하는 값을 구할 수 있다. 이는 수식15에 나와 있다.
수식14 FORWARD/BACKWARD PROBABILITY EXAMPLE
수식15 COMPLETE PATH PROBABILITY EXAMPLE
6. Likelihood Computation
우리의 관심은 입력 음성 피처 시퀀스 \(\mathbf{x}\)가 주어졌을 때 레이블 시퀀스 \(\mathbf{l}\)이 나타날 확률, 즉 가능도(likelihood)를 최대화하는 모델 파라미터(parameter)를 찾는 데 있다(Maximum Likelihood Estimation). 입력 음성 피처의 각 프레임에 대해서 모두 레이블이 있다면 지금까지 어렵사리 전방 확률이니, 후방 확률이니 하는 값들을 구할 필요 없이 네트워크 마지막 레이어의 출력인 음소 확률 벡터에서 정답 레이블에 관련된 확률들을 높여주면 그만일 것이다(=MLE=Cross Entropy 최소화). 하지만 우리가 가진 데이터는 입력 음성 피처 시퀀스 \(\mathbf{x}\)와 레이블 시퀀스 \(\mathbf{l}\)뿐이다. 둘의 길이가 다르기 때문에 크로스 엔트로피를 적용할 수 없다. 그래서 이 먼 길을 돌아오게 된 것이다.
가능도를 최대화하려면 먼저 가능도 값을 구해야 한다. CTC 문제에서 가능도는 입력 데이터 시퀀스 \(\mathbf{x}\)가 주어졌을 때 blank 없는 원래 레이블 시퀀스 \(\mathbf{l}\)이 나타날 확률을 가리킨다. 지금까지 제시했던 예시 기준으로 하면 h,e,l,l,o가 나타날 확률이다. 이와 별개로 \(\mathbf{l}^{\prime }\)은 blank가 포함된 레이블 시퀀스인데, 가능도, 즉 h,e,l,l,o가 나타날 확률을 구하려면 hel-lo--에서부터 --hel-lo에 이르는 \(\mathbf{l}^{\prime }\)에 관한 모든 가능한 경로들(그림12에서 회색 화살표의 모든 경우의 수)의 확률을 모두 고려(sum)해야 한다.
그런데 가능도 계산 역시 전방 확률과 후방 확률이 있으면 편히 구할 수 있다. 우선 수식15 계산 결과는 blank가 포함된 레이블 시퀀스 \(\mathbf{l}^{\prime }\) 가운데 \(t=3\) 시점에 상태 \(h\)를 지나는 경로들에 대한 확률이다. 이 경로들은 전체 경로 가운데 일부에 해당한다(그림11 참조). \(\mathbf{l}^{\prime }\) 관련 전체 경로의 확률 합이 가능도인데, \(t=3\)을 기준으로 가능도를 구한다고 하면 그림12의 파란색으로 칠한 다섯 칸에 해당하는 Complete Path 확률을 모두 더한 값이 된다. 이는 수식16과 같다(이해를 돕기 위해 상태 인덱스 대신 h, -, e 따위로 직접 표현하였다).
그림12 LIKELIHOOD COMPUTATION EXAMPLE

수식16 LIKELIHOOD COMPUTATION EXAMPLE
가능도 계산을 일반화한 식은 수식17과 같다. 시점(time)을 고정해 놓고 상태(state)에 대해 모두 합을 취하면 가능도가 된다. 식에서 알 수 있듯이 어떤 시점에서 계산하든 가능도 값은 동일하다. 각 시점, 상태일 확률이 조건부 독립(conditional independence)임을 가정하기 때문이다.
수식17 LIKELIHOOD COMPUTATION
7. Gradient Computation
우리는 가능도, 즉 \(p(\mathbf{l} \mid \mathbf{x})\)를 최대화하는 모델 파라미터를 찾고자 한다. 이를 위해서는 가능도에 대한 그래디언트(gradient)를 구해야 한다. 이 그래디언트를 모델 전체 학습 파라미터에 역전파(backpropagation)하는 것이 CTC 기법을 적용한 모델의 학습(train)이 된다. 가능도 계산은 보통 로그 가능도(log-likelihood)로 수행하는데, \(t\)번째 시점 \(k\)번째 상태(음소)에 대한 로그 가능도의 그래디언트는 수식18과 같다. \(\ln (x)\)를 \(x\)로 미분하면 \(1/x\)이고 가능도에 로그를 취한 것을 합성 함수라고 이해하면 체인룰(chain)에 의해 수식18 우변처럼 정리할 수 있다.
수식18 GRADIENT COMPUTATION (1)
수식18의 우변 마지막항 일부를 다시 정리한 결과는 수식19와 같다. 가능도는 수식17과 같고 상수 \(a\)에 대해 \(a/x\)를 \(x\)로 미분한 결과는 \(−a/x^{2}\)라는 점을 고려하면 수식19 우변을 이해할 수 있다. 수식19에서 \(\operatorname{lab}(1, k)\)는 \(k\)라는 음소 레이블이 \(\mathbf{l}^{\prime }\)에서 나타난 위치들을 가리킨다.
수식19 GRADIENT COMPUTATION (2)
식만 봐서는 감이 잘 안올테니 바로 예시를 보자. 그림13에서 구하고자 하는 것은 \(\partial p(\ln (\mathbf{1} \mid \mathbf{x})) / \partial y_{h}^{3}\)이다. 바로 파란색이 칠해져 있는 칸에 해당하는 그래디언트이다. 이 값을 구하려면 우선 가능도 \(p(\mathbf{l} \mid \mathbf{x})\)부터 구해야 한다. 수식20과 같다.
그림13 GRADIENT COMPUTATION EXAMPLE (1)

수식20 GRADIENT COMPUTATION EXAMPLE (1)
수식18의 로그 가능도에 대한 그래디언트를 구하기 위해서는 수식19의 가능도에 대한 그래디언트를 구해야 한다. 가능도에 대한 그래디언트는 수식20을 \(y_{h}^{3}\)으로 편미분한 결과이다. 수식20 우변에서 \(y_{h}^{3}\)과 관련된 항은 첫 번째 항뿐이기 때문에 나머지는 상수 취급해서 소거할 수 있다. 다시 말해 h라는 음소 레이블이 \(\mathbf{l}^{\prime }\)에서 나타난 위치(2)에 해당하는 항만 남긴다는 이야기이다. 수식21에서 구한 값은 수식18에 대입해 최종적으로 로그 가능도에 대한 그래디언트를 계산한다.
수식21 GRADIENT COMPUTATION EXAMPLE (1)
그림14에서 구하고자 하는 것은 \(\partial p(\ln (\mathbf{l} \mid \mathbf{x})) / \partial y_{l}^{5}\)이다. 바로 파란색이 칠해져 있는 두 개 칸에 해당하는 그래디언트이다. 이 값을 구하려면 우선 가능도 \(p(\mathbf{l} \mid \mathbf{x})\)부터 구해야 한다. 수식22와 같다.
그림14 GRADIENT COMPUTATION EXAMPLE (2)

수식22 GRADIENT COMPUTATION EXAMPLE (2)
가능도에 대한 그래디언트는 수식22를 \(y_{l}^{5}\)로 편미분한 결과이다. 수식22 우변에서 \(y_{l}^{5}\)과 관련된 항은 첫 번째 항과 두 번째 항이기 때문에 나머지는 상수 취급해서 소거할 수 있다. 다시 말해 l이라는 음소 레이블이 \(\mathbf{l}^{\prime }\)에서 나타난 위치(6, 8)에 해당하는 항만 남긴다는 이야기이다. 수식23에서 구한 값은 수식18에 대입해 최종적으로 로그 가능도에 대한 그래디언트를 계산한다.
수식23 GRADIENT COMPUTATION EXAMPLE (2)
8. Rescaling
지금까지 CTC에 대한 핵심적인 설명을 마쳤다. 단 CTC 저자에 따르면 앞의 챕터 방식대로 전방 확률과 후방 확률을 계산하게 되면 그 값이 너무 작아져 언더플로(underflow) 문제가 발생한다고 한다. 이에 수식24와 수식25와 같은 방식으로 전방 확률과 후방 확률 값을 리스케일링(rescaling)해 준다. 그래디언트 역시 리스케일한 전방/후방 확률을 기준으로 계산하게 된다.
수식24 RESCALED FORWARD PROBABILITY
수식25 RESCALED BACKWARD PROBABILITY
9. Decoding
CTC로 학습한 모델의 출력은 확률 벡터 시퀀스이므로 그 결과를 적절히 디코딩(decoding)해 주어야 한다. 가장 간단한 방법은 Best Path Decoding이라는 기법이다. 시간 축을 따라 가장 확률값이 높은 레이블을 디코딩 결과로 출력하는 방법이다.
그림15는 CTC로 학습한 모델이 출력한 확률 벡터 시퀀스를 시간 축을 따라 쭉 이어붙인 것이다. 가로축은 시간(time), 세로축은 음소를 나타낸다. 가로축을 보니 입력 음성 피처 시퀀스의 길이가 30이다. Best Path Decoding 방식으로 그림15를 디코딩하면 ---B-OO--XXX-__--BBUUNN-NI--->이 된다.
그림15 BEST PATH DECODING

Prefix Decoding은 매 스텝마다 가장 확률값이 높은 prefix를 디코딩 결과로 출력하는 것이다. 그림16과 같다. 그림16의 첫 번째 스텝에서 가장 확률값이 높은 prefix는 X이다. 그런데 X의 확률값(0.7)은 두 번째 스텝에서 각 상태가 지니는 확률의 합\((p(X)=0.1, p(Y)=0.5, p(e)=0.1)\)과 같다. X의 확률값(0.7)은 \(t=1\) 시점에 상태가 X일 확률을 가리키는데, 이는 앞서 설명한 Forward/Backward Algorithm으로 계산 가능하다. 어쨌든 그림16와 같은 예시일 때 Prefix Decoding 결과는 XYe가 된다.
그림16 PREFIX DECODING

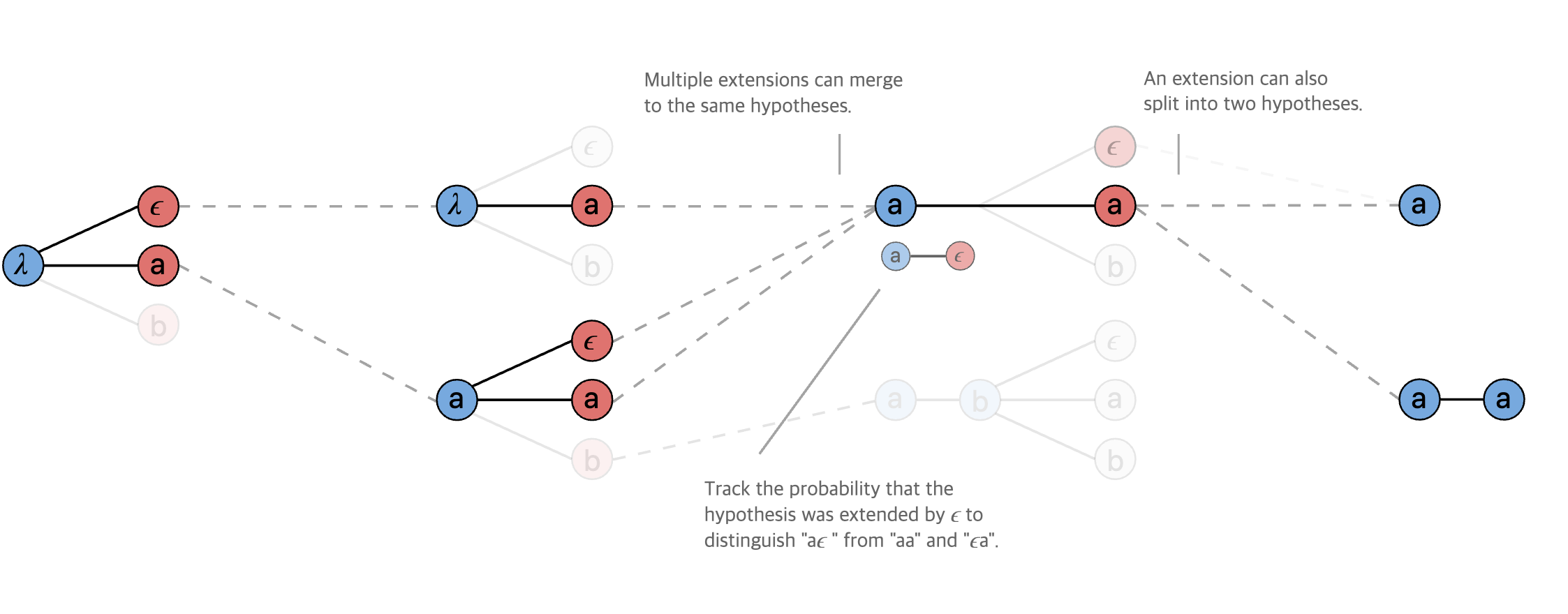
Beam Search는 매 스텝마다 가장 확률이 높은 후보 시퀀스를 beam 크기만큼 남겨서 디코딩하는 방법이다. 그림17은 beam 크기가 3일 때 Beam Search의 일반적인 디코딩 과정을 도식적으로 나타내고 있다. 시간이 아무리 흘려도 살아남는 후보 시퀀스 개수는 beam 크기가 된다. 그림18과 그림19은 CTC로 학습한 모델의 Beam Search 과정을 나타낸다. 일반적인 Beam Search와 거의 유사하나 디코딩 과정에서 여러 번 등장한 음소를 합치거나 blank 등을 적절히 처리해 준다.
그림17 BEAM SEARCH (1)
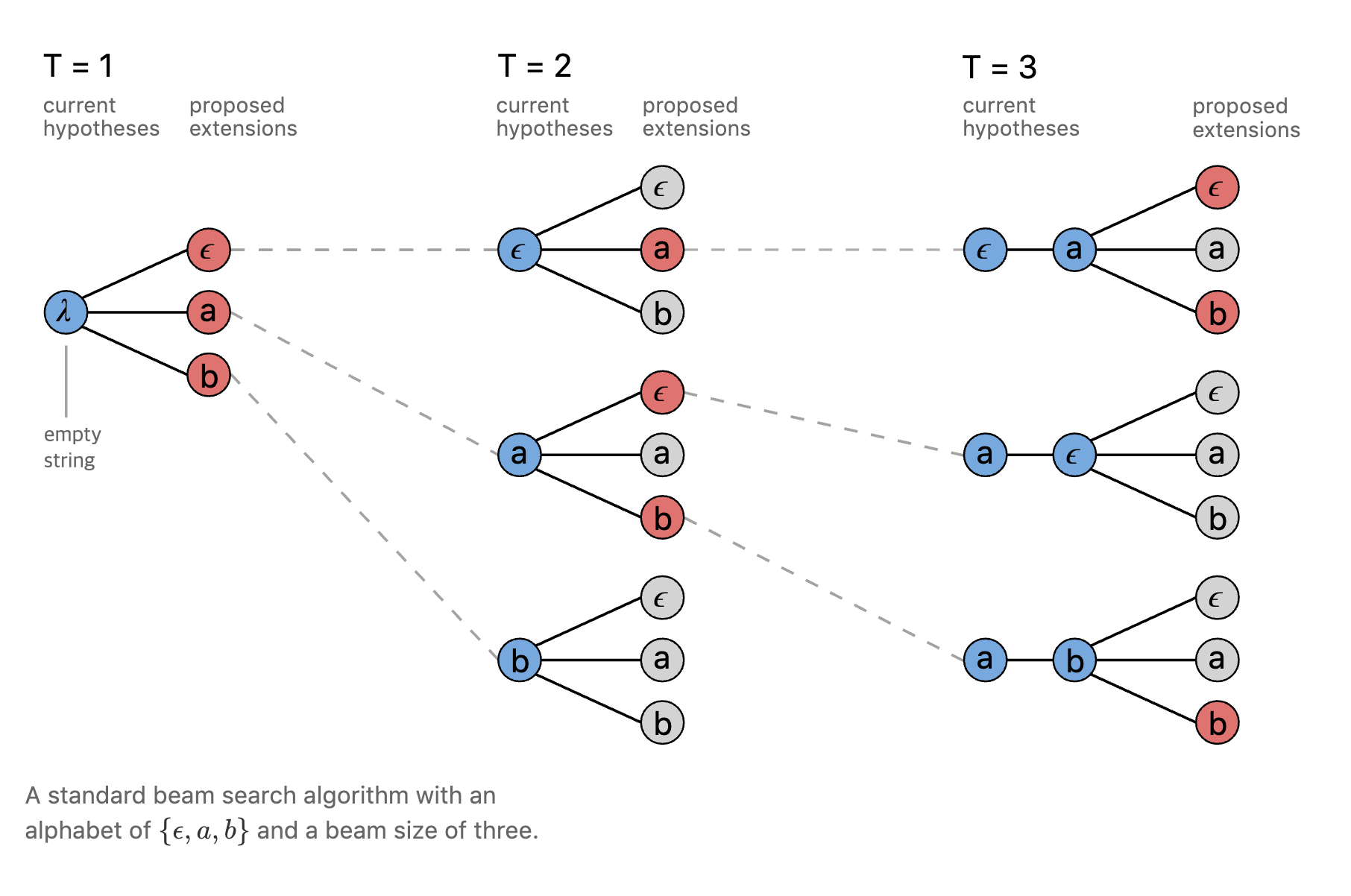
그림18 BEAM SEARCH (2)

그림19 BEAM SEARCH (3)
10. Properties
그림20은 프레임 단위 레이블로 학습한 음성 인식 모델과 CTC로 학습한 모델 간 차이를 나타내는 그림으로 CTC 원저자가 작성한 것이다. 저자에 따르면 dh라는 음소의 경우 프레임 단위 모델은 정답을 잘 맞췄지만 다른 음소와의 구분이 잘 되지 않았다. 그에 반해 CTC 모델은 구분이 잘 되어 있는 걸 확인할 수 있다. 아울러 CTC 모델은 프레임 단위 모델 대비 음소 확률 분포가 뾰족(spiky)하고 희소(sparse)하다.
그림20 ACTIVATIONS

하지만 그림20이 역설적이게도 CTC 모델의 단점을 드러낸 모델이 아닌가 싶다. 입력 음성 피처 시퀀스별로 레이블을 부여(Forced Alignment)하는 태스크에는 CTC가 제대로 작동하지 않을 염려가 있다고 생각되기 때문이다. 실제로 CTC 모델이 s 음소를 인식 결과로 리턴할 수 있는 구간은 프레임 단위 모델 대비 짧은 편이다.