2. Wav2Vec
Info
뉴럴 네트워크 기반 피처 추출 기법 가운데 하나인 Wav2Vec/VQ-Wav2Vec 모델을 살펴본다. 사람의 개입 없이 음성 특질을 추출하는 방법을 제안해 주목을 받았다. 다만 음성 특질의 품질이 PASE보다는 낮은 경향이 있고 아직은 정립이 되지 않은 방법론이라 생각돼 그 핵심 아이디어만 간략하게 일별하는 방식으로 정리해 보자.
1. Wav2Vec
Wav2Vec의 전체 아키텍처는 그림1과 같다. Wav2Vec은 크게 encoder network \(f\)와 context network \(g\) 두 개 파트로 구성돼 있다. 둘 모두 컨볼루션 뉴럴 네트워크(convolutional neural network)이다.
encoder network \(f\)는 음성 입력 \(\mathcal{X}\)를 hidden representation \(\mathcal{Z}\)로 인코딩하는 역할을 수행한다. context network \(g\)는 \(\mathcal{Z}\)를 context representation \(\mathcal{C}\)로 변환한다. Wav2Vec 학습을 마치면 \(\mathcal{C}\)를 해당 음성의 피처로 사용한다.
그림1 WAV2VEC
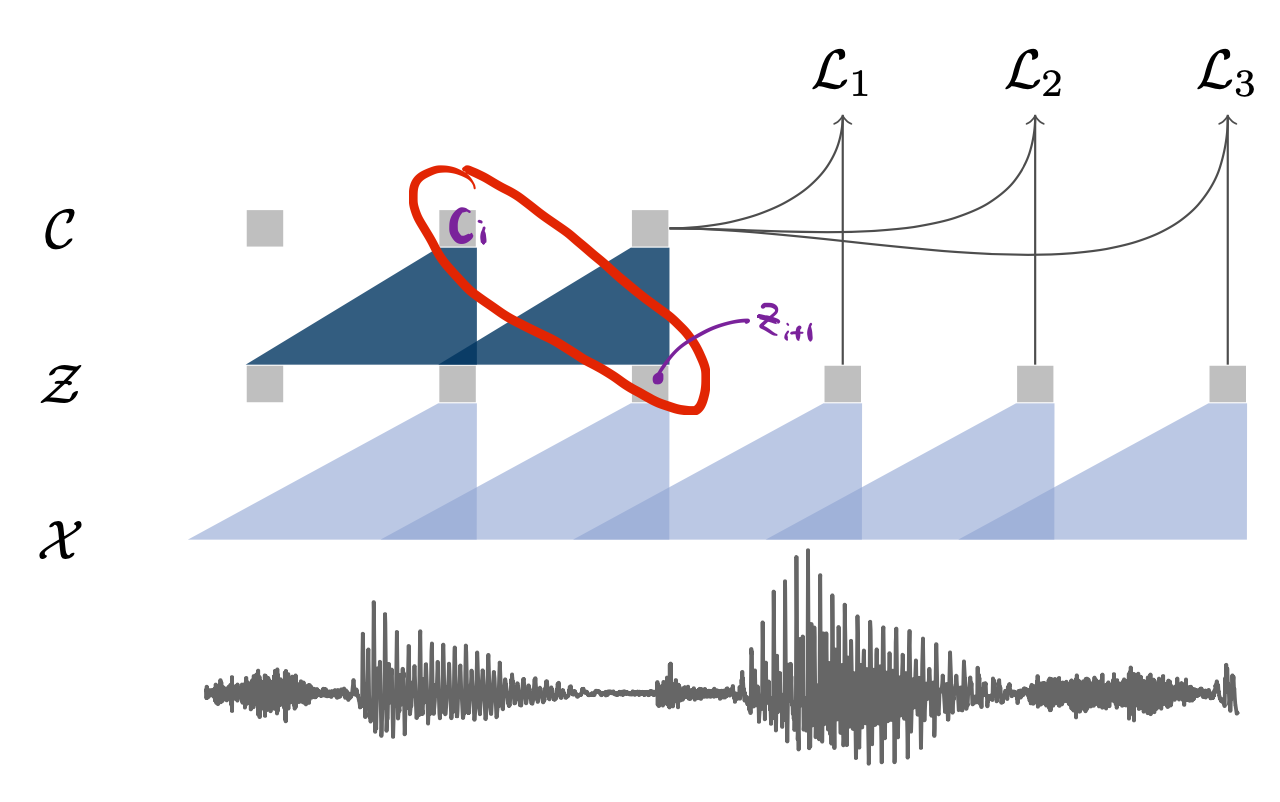
Wav2Vec은 Word2Vec처럼 해당 입력이 포지티브 쌍인지 네거티브 쌍인지 이진 분류(binary classification)하는 과정에서 학습된다. 포지티브 쌍은 그림1처럼 입력 음성의 \(i\)번째 context representation \(\mathcal{C}_{i}\)와 \(i+1\)번째 hidden representation \(\mathcal{Z}_{i+1}\)이다. 네거티브 쌍은 입력 음성의 \(i\)번째 context representation \(\mathcal{C}_{i}\)와 현재 배치의 다른 음성의 hidden representation들 가운데 랜덤으로 추출해 만든다.
학습이 진행될수록 포지티브 쌍 관계의 representation은 벡터 공간에서 가까워지고, 네거티브 쌍은 멀어진다. 다시 말해 encoder network \(f\)와 context network \(g\)는 입력 음성의 다음 시퀀스가 무엇일지에 관한 정보를 음성 피처에 잘 녹여낼 수 있게 된다.
2. VQ-Wav2Vec
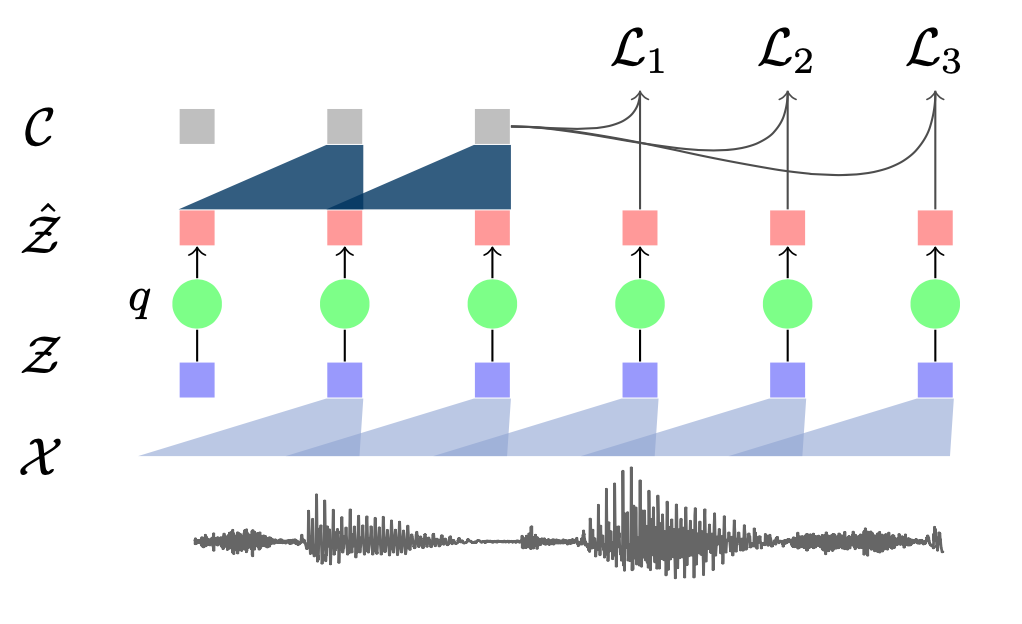
VQ-Wav2Vec은 기본적으로는 Wav2Vec의 아키텍처와 같다. 다만 중간에 Vector Quantization 모듈이 추가됐다. 그림2와 같다. encoder network \(f\)는 음성 입력 \(\mathcal{X}\)를 hidden representation \(\mathcal{Z}\)로 인코딩하는 역할을 수행한다. Vector Quantization 모듈 \(q\)는 continous representation \(\mathcal{Z}\)를 discrete representation \(\hat{\mathcal{Z}}\)로 변환한다. context network \(g\)는 \(\hat{\mathcal{Z}}\)를 context representation \(\mathcal{C}\)로 변환한다.
그림2 VQ-WAV2VEC
3. Vector Quantization
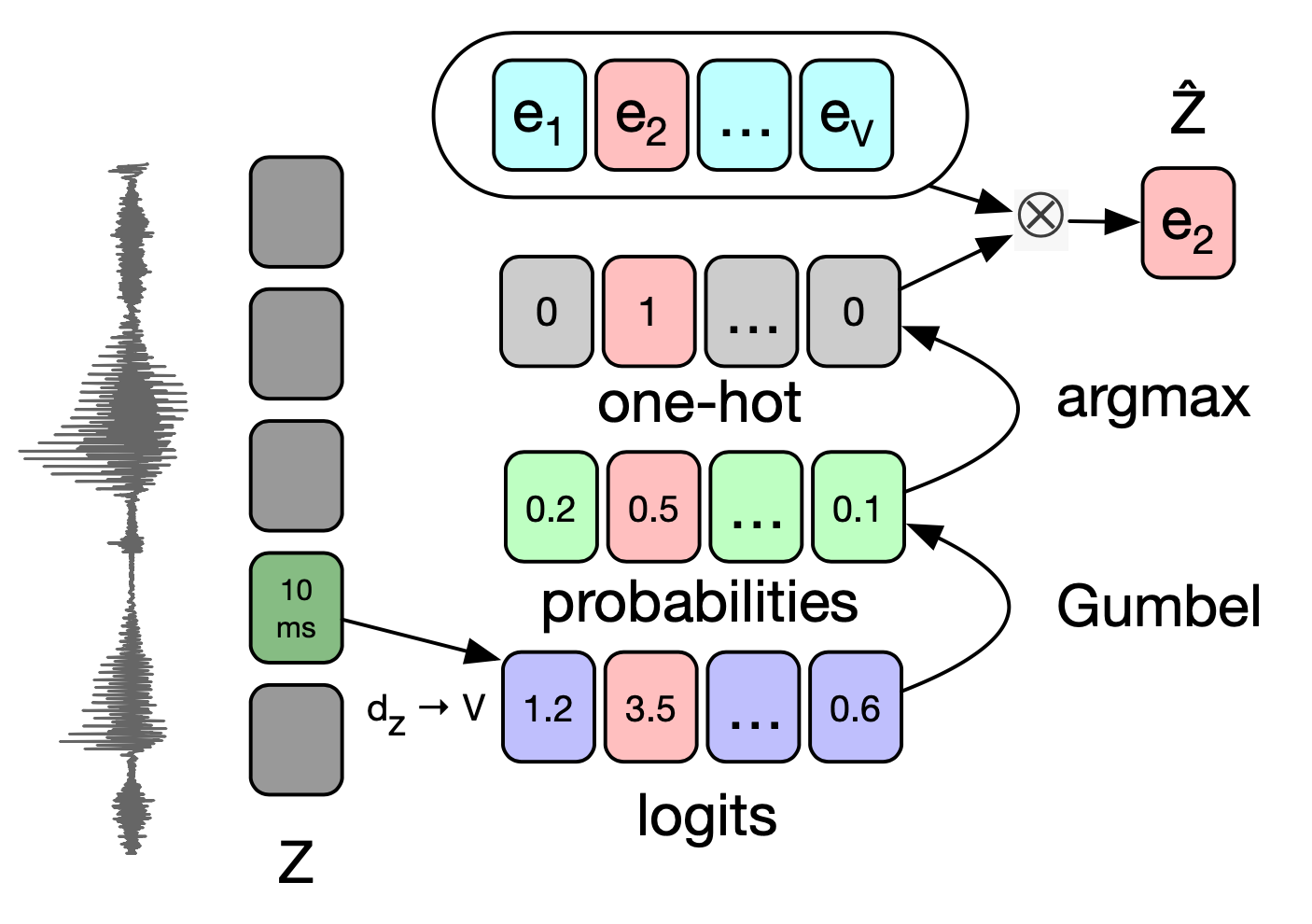
VQ-Wav2Vec의 핵심은 Vector Quantization 모듈이다. Gumbel Softmax, K-means Clustering 두 가지 방식이 제시됐다. 그림3은 Gumbel Softmax를 도식화한 것이다. 우선 \(\mathcal{Z}\)를 선형변환해 logit을 만든다. 여기에 Gumbel Softmax와 argmax를 취해 원핫 벡터를 만든다. 연속적인(continous) 변수 \(\mathcal{Z}\)가 이산(discrete) 변수로 변환됐다. 이것이 바로 Vector Quantization이다.
이후 Embedding matrix를 내적해 \(\hat{\mathcal{Z}}\)를 만든다. 결과적으로는 Vector Quantization으로 \(V\)개의 Embedding 가운데 \(e_{2}\)를 하나 선택한 셈이 되는 것이다.
그림3 GUMBEL SOFTMAX
그런데 여기에서 하나 의문이 있다. argmax는 미분이 불가능한데 어떻게 이 방식으로 전체 네트워크를 학습할 수 있을까? Gumbel Softmax를 파이토치로 구현한 코드를 보면 이해할 수 있다. 코드1을 보자.
코드1 GUMBEL SOFTMAX
import torch
import torch.nn as nn
import torch.nn.functional as F
from torch.autograd import Variable
def sample_gumbel(shape, eps=1e-20):
U = torch.rand(shape).cuda()
return -Variable(torch.log(-torch.log(U + eps) + eps))
def gumbel_softmax_sample(logits, temperature):
y = logits + sample_gumbel(logits.size())
return F.softmax(y / temperature, dim=-1)
def gumbel_softmax(logits, temperature):
"""
input: [*, n_class]
return: [*, n_class] an one-hot vector
"""
y = gumbel_softmax_sample(logits, temperature)
shape = y.size()
_, ind = y.max(dim=-1)
y_hard = torch.zeros_like(y).view(-1, shape[-1])
y_hard.scatter_(1, ind.view(-1, 1), 1)
y_hard = y_hard.view(*shape)
return (y_hard - y).detach() + y
gumbel_softmax의 리턴값, (y_hard - y).detach() + y에 주목하자. 순전파(forward computation)에서는 argmax가 취해져 원핫 벡터가 된 y_hard만 다음 레이어 계산에 넘겨준다. 역전파(backward computation)에서는 소프트맥스가 취해진 확률 벡터인 y에만 그래디언트가 흘러간다.
VQ-Wav2Vec 저자들은 K-means Clustering 방식으로도 Vector Quantization을 수행했다. \(\mathcal{Z}\)와 Embedding Matrix 각각의 벡터와 유클리디안 거리를 계산한다. 여기에서 가장 가까운 Embedding Vector를 하나 선택(그림4 예시에서는 \(e_{2}\)가 선택)해 다음 계산으로 넘긴다.
그림4 K-MEANS CLUSTERING
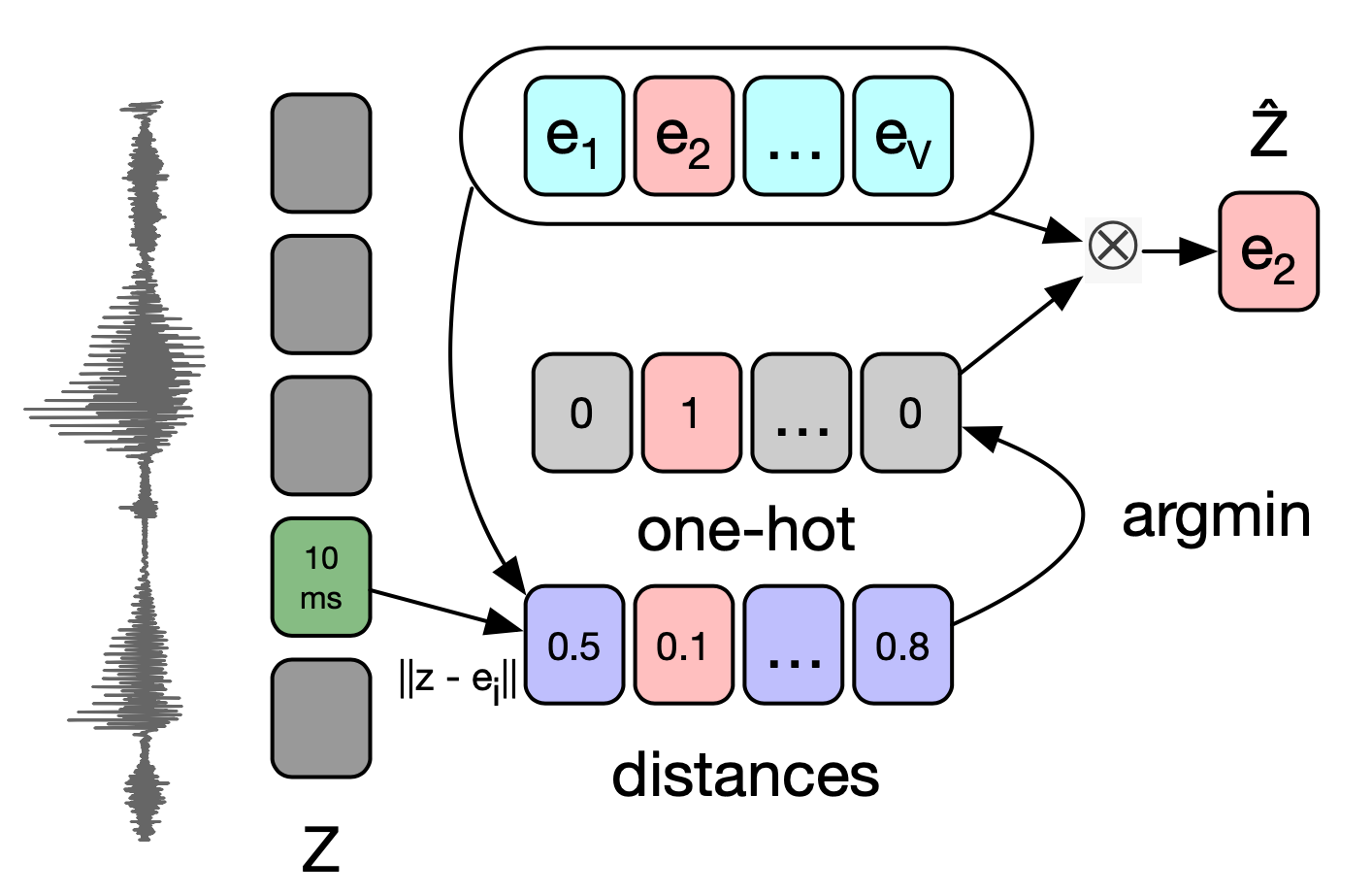
argmin 역시 미분이 불가능한데, Gumbel Softmax 때처럼 순전파와 역전파 과정을 섬세하게 설계하면 미분 가능헤가 만들 수 있다.