7. Training Technics
Info
히든 마코프 모델(Hidden Markove Model) + 가우시안 믹스처 모델(Gaussian Mixture Model) 기반 음향 모델 관련 중요 학습 테크닉들을 살펴본다.
1. Embedded Training
히든 마코프 모델(Hidden Markov Model) 기반의 음향 모델(Acoustic Model)은 상태(state)를 단어(word) 대신 음소(phone)보다 작은 subphone 단위로 모델링한다. 음성 신호는 아주 짧은 시간 단위(대개 25ms 내외)로 잘게 쪼개어 프레임 단위로 분석하는데(주파수 도메인에서 stationary 가정 하에 Framing 실시), 이 작은 프레임 단위 관측치(observation)에 대응할 만한 상태(state)는 음소보다 더 작은 단위일 것이기 때문이다.
그런데 우리가 확보한 학습 데이터는 음성 신호(wave file)와 그에 대응하는 단어 수준 스크립트(trascript)뿐이다. 물론 음소 수준보다 더 작은 단위로 스크립트를 만들 수도 있겠으나 레이블링하는 데 비용이 많이 들고, 사람은 음소 단위로 말소리를 인식하기 때문에 이보다 더 작은 단위의 레이블링 작업은 신뢰하기 어렵다.
이 때문에 히든 마코프 모델을 구축할 때 학습 과정에서 입력 음성 프레임과 해당 프레임에 대응하는 상태(subphone)가 정렬(align)되도록 구조를 설계해야 한다. 이렇게 음성 신호와 단어 수준 스크립트만 가지고, 짧은 단위의 입력 프레임과 상태(subphone)가 학습 과정에서 자동으로 정렬되도록 유도하는 기법을 임베디드 트레이닝(Embedded Training)이라고 한다.
히든 마코프 모델의 학습 대상 파라미터(parameter)는 전이 행렬(transition matrix) \(A\)와 방출 확률 모델(emission probability estimator) \(B\)이다. 임베디드 트레이닝 기법을 쓰면 음소 혹은 subphone 같은 작은 단위로 스크립트를 만들 필요가 없이 단어 수준 스크립트만 있으면 된다. 학습 과정에서 자동 정렬이 되기 때문이다.
히든 마코프 모델에서 임베디드 트레이닝이 가능한 이유는 히든 마코프 모델의 구조적 특성 때문이다. 히든 마코프 모델은 상태 시퀀스(state sequence)가 은닉(hidden)되어 있다고 가정한다. 짧은 단위의 입력 프레임(observation)에 대응하는 실제 상태(subphone)가 어떤 것인지 몰라도 학습 과정에서 자동으로 추론이 된다.
여기에 발음 사전(pronunciation lexicon)의 도움을 받아 전이(transition)의 제약(self-loop, left-to-right)을 두면 화자나 상황에 따라서 특정 음소를 길게 발음할 수도 있고 짧게 말할 수 있는 점을 고려한 모델을 구축할 수 있게 된다. 임베디드 트레이닝을 수행하기 위해 필요한 준비물은 미리 정의해둔 음소 집합(phoneset), 발음 사전, 음성 파일(wave file)들과 그에 대응하는 단어 수준 스크립트(transcript) 네 가지이다. 수행 과정은 다음과 같다.
1] 우선 단어 수준 스크립트와 발음 사전(Grapheme To Phoneme)을 가지고 상태를 subphone으로 설정한 히든 마코프 모델을 빌드(학습할 준비)한다. 해당 스크립트에 대응하는 음성 파일 역시 MFCC로 만들어 둔다.
2] 전이 행렬 \(A\)를 초기화한다. 전이는 두 가지만 가능하도록 세팅한다. 발음 사전을 참고해 self-loop에 해당하는 케이스를 0.5, 다음 subphone으로 전이하는 경우를 0.5로 설정한다. 나머지 케이스에 대해서는 0으로 둔다(Baum-Welch Algorithm에 따르면 전이 확률 업데이트시 이전 전이 확률을 고려하므로 초기 0으로 세팅된 전이 확률은 학습이 끝날 때까지 0으로 남아 있다).
3] 방출 확률 모델 \(B\)를 초기화한다. 가우시안 믹스처 모델인 경우 파라미터는 각 가우시안 모델의 평균 벡터와 공분산 행렬인데, 이를 음성 데이터(MFCC) 전체의 평균과 공분산으로 설정해 준다. 따라서 각 상태에 대응하는 가우시안 믹스처 모델들은 아무런 사전 정보가 없이 학습을 시작하는 셈이 된다.
4] Baum-Welch Algorithm을 수회 반복 수행한다.
2. Viterbi Training
Baum-Welch Algorithm은 상정 가능한 모든 상태에 해당하는 경로(acumulate counts by a sum over all paths)를 고려하기 때문에 계산복잡성이 높다. 이에 가장 확률값이 높은 경로 하나(the most probable path)만 업데이트해 계산량을 확 줄이는 기법을 쓴다. 이를 비터비 트레이닝(Viterbi Training)이라고 한다.
비터비 트레이닝으로 학습하는 기법을 Forced Alignment 혹은 Forced Viterbi Alignment라고도 부른다. 학습 도중 비터비 기법으로 찾은 상태열을 정답이라고 보고 입력 음성 프레임과 상태(subphone)을 강제로 정렬(forced alignment)한다는 취지에서 이런 이름이 붙은 것 같다.
비터비 트레이닝은 학습 기법으로, 디코딩 때 쓰는 비터비 디코딩(Viterbi Decoding)과는 다른 개념이니 혼동이 없어야겠다. 비터비 트레이닝과 비터비 디코딩이 다른 점은 후자가 단어 수준의 최적 상태열까지 찾아야 하는 반면 전자는 상태(subphone) 수준의 최적 상태열만 찾으면 된다는 점이다.
학습 과정 도중 비터비 기법으로 하나의 최적 상태열을 찾았다고 가정해 보자. 이 경우 정답 상태(state)를 완벽하게 알고 있다고 전제한 상황의 히든 마코프 모델 학습이 가능해진다. 전이 확률은 이전 상태에서 다음 상태로 전이하는 케이스들을 각각 세어서 확률값을 업데이트하면 된다. 방출 확률 모델을 가우시안 믹스처 모델로 두었을 경우 각 관측치(\(o_{t}\))를 해당 상태(\(q_{j}\))에 대응하는 가우시안 믹스처 모델의 학습 데이터로 두면 된다. 이해를 돕기 위해 믹스처가 아닌 가우시안 모델이라고 가정하면 가우시안 파라미터 가운데 하나인 평균 벡터의 업데이트는 수식1처럼 하면 된다.
수식1 가우시안 모델의 비터비 트레이닝
비터비 트레이닝은 히든 마코프 모델 + 멀티 레이어 퍼셉트론(Multi-Layer Perceptron, MLP), 히든 마코프 모델 + 서포트 벡터 머신(Support Vector Machine, SVM) 같은 하이브리드 모델의 임베디드 트레이닝에도 적용할 수 있다고 한다. 앞서 임베디드 트레이닝 챕터에서 설명했던 것처럼 전이 행렬 \(A\)와 방출 확률 \(B\)를 초기화한 뒤 비터비 트레이닝 방식으로 Baum-Welch Algorithm을 수회 반복한다. 비터비 트레이닝은 MLP/SVM은 초기에 랜덤에 가까운 모델이고 학습 과정 중에 단 하나의 베스트 경로만을 대상으로 업데이트를 하기 때문에 학습 초기엔 굉장히 불안정할 수 있다. 하지만 에폭(epoch)이 반복될 수록 점차 입력 음성 프레임과 상태(subphone) 사이의 정렬(alignment)이 점차 정확해 진다.
3. Vector Quantization
관측치가 이산적(discrete)이지 않고 연속적(continuous)일 경우 히든 마코프 모델에서 방출 확률(emission probability)을 계산하기가 까다롭다. 이산 변수의 경우라면 해당 상태에 대응하는 관측치들의 개수를 세어서 방출확률 값을 추정하면 될텐데, 연속 변수라면 그 개수를 셀 수 없기 때문에 \(j\)번째 상태일 때 \(t\)번째 관측치가 관찰될 방출 확률, 즉 \(P\left(o_{t} \mid q_{j}\right)\)을 추정하기 어렵다. 연속 변수에 대한 방출 확률 계산을 위해 제안된 모델이 바로 가우시안 믹스처 모델(Gaussian Mixture Model)이다.
연속 변수에 대한 방출확률 계산을 위해 쓸 수 있는 방법이 또 있다. 벡터 양자화(Vector Quantization) 기법이다. 벡터 양자화란 연속 변수인 벡터를 이산 변수로 바꾸는 과정을 가리킨다. 그 컨셉은 그림1과 같다.
그림1 VECTOR QUANTIZATION
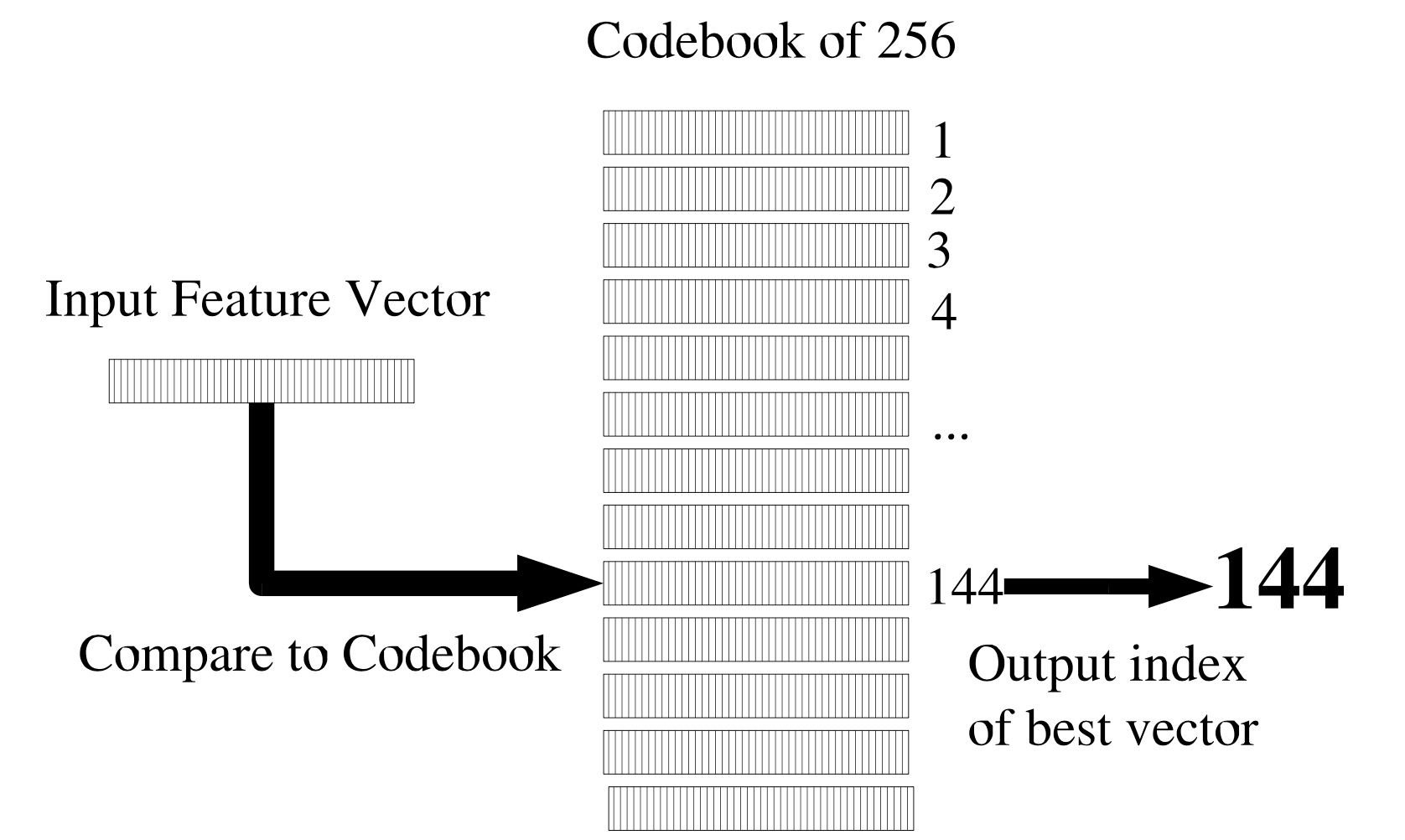
그림1에서 Codeword이란 비교 대상이 되는 벡터이다. 이들 Codeword를 모두 모은 집합을 Codebook이라고 한다. 그림1의 경우 Codebook은 256개의 Codeword들로 구성돼 있고, 이처럼 벡터 양자화를 수행한다면 모든 입력 벡터를 0~255의 정수로 양자화(8-bit)할 수 있다.
입력 피처 벡터(Input Feature Vector)가 들어왔을 때 각각의 Codeword와 거리(distance)를 계산한다. 예컨대 이 입력벡터가 144번째 Codebook와 거리가 가장 가까웠다고 가정해 보자. 그러면 벡터 양자화의 결과는 해당 Codebook의 인덱스(144)가 된다.
벡터 양자화를 수행하기 위해서는 먼저 Codebook을 만들어야 한다. 학습 데이터 모든 벡터를 사용자가 정한 개수의 군집(cluster)으로 클러스터링을 수행한다. 이후 각 클러스터를 대표하는 벡터를 고르고 이 벡터를 해당 클러스터에 대한 Codeword로 삼는다. 대개 K-means Clustering을 사용한다고 한다.
Codebook을 만든 이후엔 벡터 양자화를 수행할 수 있다. 양자화 결과는 거리(distance) 측정 방법에 따라 크게 달라진다. 벡터 양자화를 수행하고 나면 연속 변수가 이산 변수로 변환된 상태가 되는데, 이후 기존 이산 변수에 대한 방출 확률을 추정했던 것처럼 히든 마코프 모델을 학습하면 된다.