3. Baum-Welch Algorithm
Info
히든 마코프 모델(Hidden Markov Model)을 학습하는 기법 가운데 하나가 '바움-웰치 알고리즘(Baum-Welch Algorithm)'이다. 바움-웰치 알고리즘은 EM 알고리즘의 일종인데, 이번 글에서 자세히 살펴본다.
1. 상태를 알 경우의 HMM 학습
예컨대 당신이 100년 전 기후를 연구하는 학자인데, 주어진 정보는 당시 아이스크림 소비 기록(관측치, observation)뿐이라고 치자. 이 정보 만으로 당시 날씨(상태, state)가 더웠는지(HOT), 추웠는지(COLD)를 알고 싶은 것이다. 그런데 운이 좋게도 우리는 관측치뿐 아니라 상태까지 포함된 데이터를 확보했다고 가정해 보자. 그림1과 같다.
그림1 상태와 관측치가 모두 주어진 학습 데이터
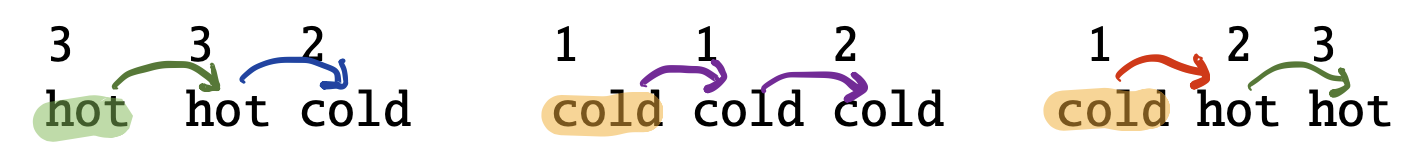
그림1과 같이 상태(state)와 관측치(observation)를 모두 알고 있을 경우 히든 마코프 모델을 학습(parameter estimation)하기가 대단히 쉬워진다. 각각에 해당하는 경우를 일일이 세기만 하면 된다. 우선 초기 상태 분포(initial probability distribution) \(\pi\)는 수식1과 같다. 전체 3건의 데이터 가운데 초기 상태가 HOT인 경우는 1가지, COLD인 경우는 2가지이기 때문이다.
수식1 초기 상태 분포

그림1로부터 전이 확률을 구하는 과정 역시 간단하다. 각 케이스를 세면 된다. 예시로 \(P(\text {COLD} \mid \text {HOT})\)를 구해보자. 전체 데이터 가운데 HOT에서 출발하는 경우(number of transitions from HOT)는 모두 3가지이다(1번 데이터: HOT HOT COLD, 1번 데이터: HOT HOT COLD, 3번 데이터: COLD HOT HOT). 현재 상태가 HOT이고 다음 상태가 COLD인 경우(number of transitions from HOT to COLD)는 1가지이다(1번 데이터: HOT HOT COLD). 수식2에 따라 \(P(\text {COLD} \mid \text {HOT})\)를 구하면 그 값은 \(1 / 3\)이 된다. 이를 확장해서 모두 구하면 수식3과 같다.
수식2 I번째 상태에서 J번째 상태로 전이할 확률
수식3 전이 확률 분포
마지막으로 방출 확률을 구해보자. 예시로 \(P(3 \mid \text {HOT})\)을 계산해 보자. 우선 전체 데이터에서 상태가 HOT이 몇 번 등장했는지(numebr of times in HOT) 센다. 총 4회(HOT은 1번 데이터에 2회, 3번 데이터에 2회)이다. 이번엔 상태가 HOT일 때 관측치가 3인 경우가 몇 번 있었는지 센다. 총 3회(1번 데이터 첫 번째 step, 1번 데이터 두 번째 step, 3번 데이터 세 번째 step)이다. 수식4에 따라 \(P(3 \mid \text {HOT})\)를 구하면 그 값은 \(3 / 4\)가 된다. 이를 확장해서 모두 구하면 수식5와 같다.
수식4 J번째 상태에서 \(v_{k}\)가 관측될 방출 확률
수식5 방출 확률 분포
2. 상태를 모를 경우의 HMM 학습
문제는 상태(state)는 은닉(hidden)되어 알 수 없다는 점이다. 그림2를 예로 들면 \([3,3,2]\), \([1,1,2]\), \([1,2,3]\) 같은 관측치(observation)만 데이터로 주어진 상황이다. 이 경우 관측치들이 시점(time)별로 각각 어떤 상태일지 추정하는 과정이 필요하게 된다. 이렇게 상태 추정을 마쳤다면 '관측치 각 시점에 달린 상태를 알고 있다'고 전제하고 전이 확률 \(A\)와 방출 확률 \(B\)을 구했던 앞선 챕터처럼 히든 마코프 모델의 파라미터를 계산할 수 있게 된다.
\(A\)와 \(B\) 추정값을 구하는 데 있어 핵심적인 아이디어는 수식6, 수식7과 같다. 앞선 챕터 계산 방식과 거의 유사하나 분자, 분모 계산 시 기댓값(expectation)을 쓴다는 점만 다르다. 그도 그럴 것이 우리는 관측치에 달린 상태를 모르기 때문에 말그대로 기대되는 값만 쓸 수 있지 정확한 값을 계산할 수는 없다.
수식6 I번째 상태에서 J번째 상태로 전이할 확률 추정값
수식7 J번째 상태에서 \(v_{k}\)가 관측될 방출 확률 추정값
이제 문제가 되는 것은 수식6과 수식7에 쓰이는 기댓값들을 구해야 하는 과정이 된다. 수식6과 관련해서는 \(\xi\), 수식7과 관련해서는 \(\gamma\)라는 값으로 기댓값 계산을 한다. 다음 챕터에서 차례대로 살펴보자.
3. \(\xi\) 개념과 계산 과정
전이 확률 \(A\)와 밀접한 관련을 지니는 \(\xi\)는 수식8과 같이 정의된다. 모델 \(\lambda\)와 관측치 시퀀스 \(O\)가 주어졌을 때 \(t\)번째 시점의 상태가 \(i\)이고 \(t+1\) 시점의 상태가 \(j\)일 확률이다.
수식8 \(\xi\) 정의
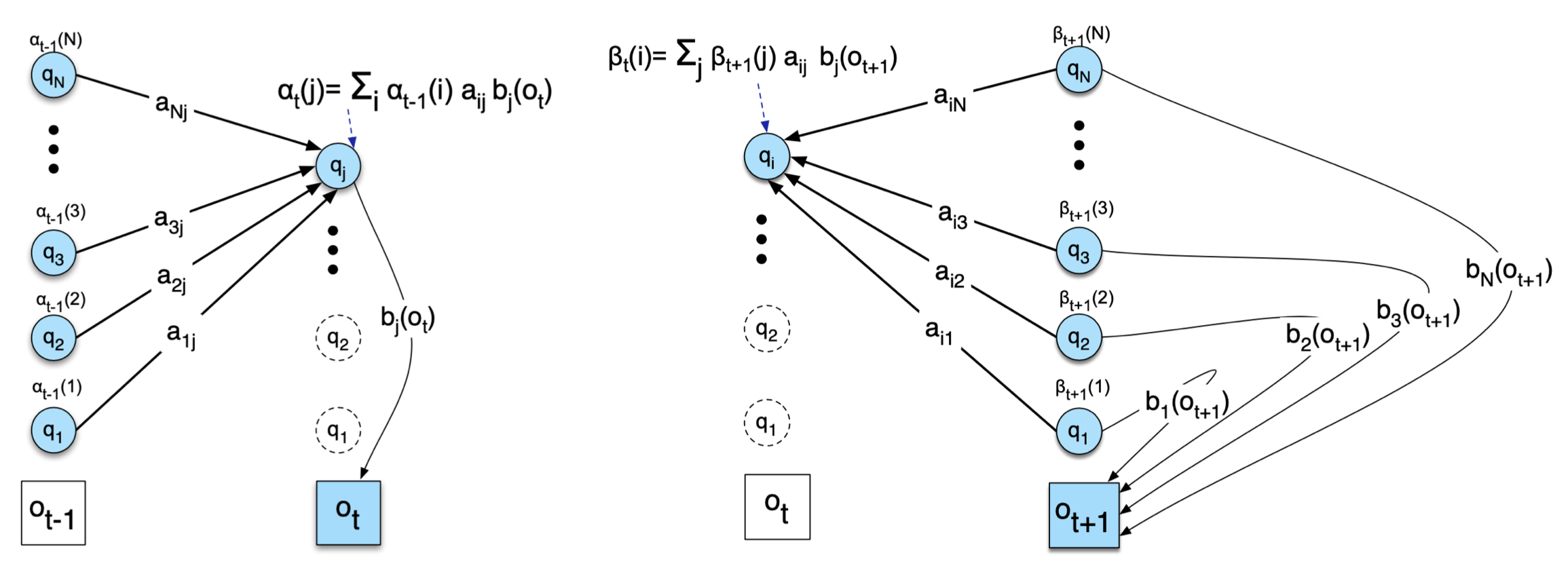
\(\xi\) 계산에 요긴하게 쓰일 수 있는 것이 전방 확률(forward probability)과 후방 확률(backward probability)이다. 전방 확률/후방 확률 수식과 개념도는 그림2와 같다. 수식8의 \(\xi\)를 조건부 확률 정의, 즉 \(P(X \mid Y, Z)=P(X, Y \mid Z) / P(Y \mid Z)\)를 활용해 전방/후방 확률 형태로 다시 쓰면 수식9와 같다.
그림2 전방 확률(좌)과 후방 확률(우)
수식9 전방/후방 확률을 활용한 \(\xi\) 계산
수식9가 어떤 의미를 지니는지 직관적으로 이해해보자. 우선 분모부터 보자. 정방 확률 \(\alpha_{t}(j)\)는 초기 상태로부터 시작해 \(t\)번째 상태가 \(j\)이고 해당 시점/상태에서 \(o_{t}\)가 관측될 모든 경우(상태 시퀀스, 관측치 시퀀스)의 수에 해당하는 가능도(likelihood)를 가리킨다. 후방 확률 \(\beta_{t}(j)\)는 종류 상태로부터 거슬러 와 \(t\)번째 상태가 \(j\)일 모든 경우의 수에 해당하는 가능도이다.
이 둘의 곱은 관측치 시퀀스 \(O\)가 주어졌을 때 \(t\)번째 시점의 상태가 \(j\)일 가능도를 가리킨다(그림3). 이를 모든 상태(\(j\))에 대해 합을 취하면 \(P(O \mid \lambda)\)이다. 즉 수식9 분모는 해당 관측치 시퀀스가 나타날 전체 가능도가 된다. 이전 글을 예로 들면 관측치(사흘 간의 아이스크림 소비 기록) \([3,1,3]\)이 나타날 확률 0.02856이 된다.
그림3 \(\xi\) 분모 이해하기

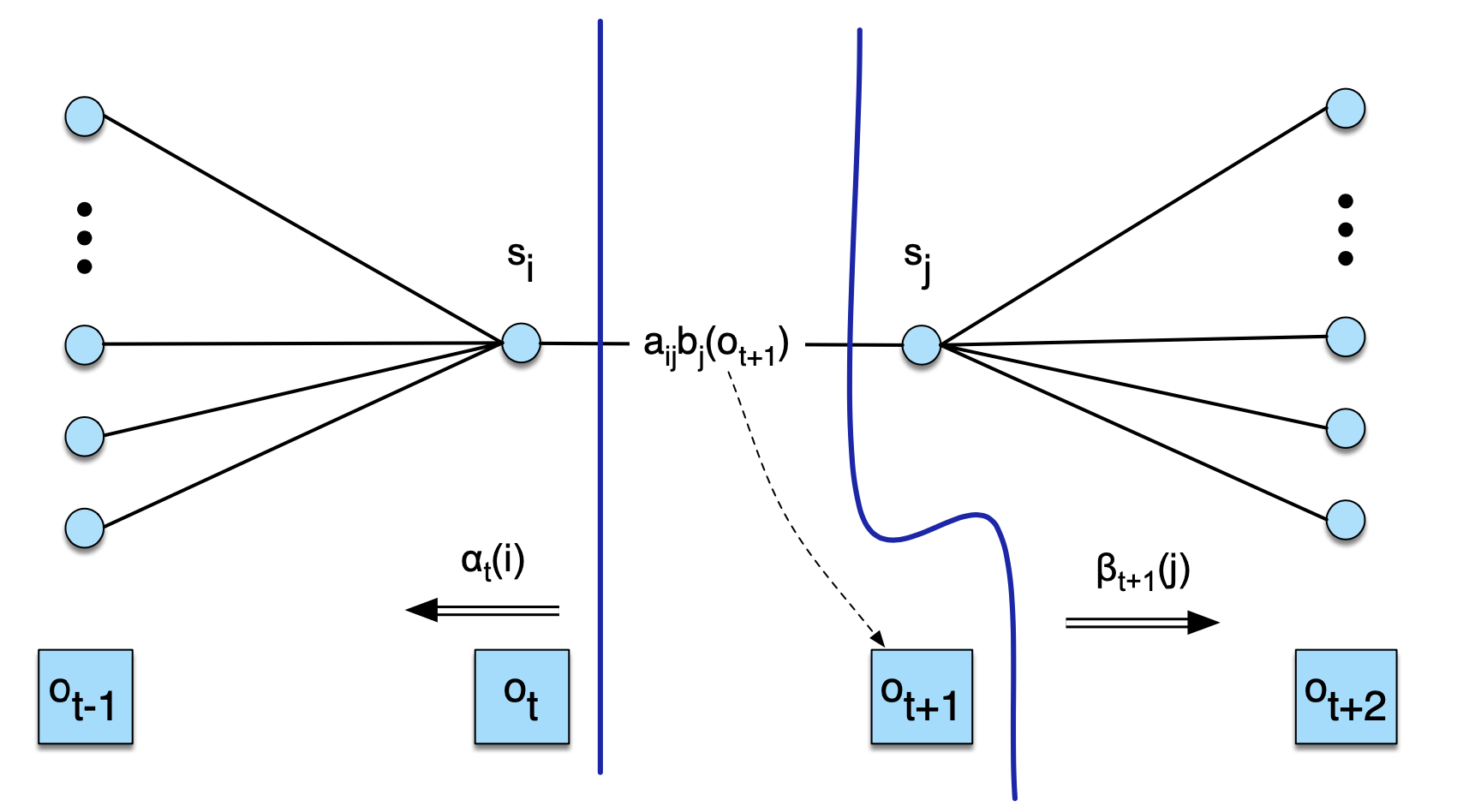
이번엔 수식9 분자를 보자. 그림4와 같이 보면 좋을 것 같다. 전방 확률 \(\alpha_{t}(i)\)는 초기 상태로부터 시작해 \(t\)번째 상태가 \(i\)이고 해당 시점/상태에서 \(o_{t}\)가 관측될 모든 경우(상태 시퀀스, 관측치 시퀀스)의 수에 해당하는 가능도이다. 후방 확률 \(\beta_{t+1}(j)\)는 종료 상태로부터 거슬러 와 \(t+1\)번째 상태가 \(j\)일 가능도이다. 이 둘 사이를 잇는 것은 \(a_{i j} b_{j}\left(o_{t+1}\right)\)인데, 각각 \(i\)번째 상태에서 \(j\)번째 상태로 전이할 확률, \(j\)번째 상태에서 \(o_{t+1}\)이 관측될 방출 확률을 가리킨다. 즉 수식9 분자는 \(t\)번째 시점에 \(i\)번째 상태이고 \(t+1\)번째 시점에 \(j\)번째 상태이며 관측치 시퀀스 \(O\)가 나타날 확률을 의미한다.
그림4 \(\xi\) 분자 이해하기
4. \(\xi\)를 바탕으로 전이 확률 \(A\) 계산하기
전이 확률 추정값을 \(\xi\)로 기술하고, 요소별로 나눠서 살펴본 결과는 수식10과 같다. \(\xi\)로 "전이의 기댓값(expected number of transition)"을 구하고, 이들 기댓값을 바탕으로 전이 확률을 업데이트한다.
수식10 I번째 상태에서 J번째 상태로 전이할 확률 추정값
\(\xi_{t}(i, j)\): 관측치 시퀀스 \(O\)가 주어졌을 때 \(t\)번째 시점의 상태가 \(i\)이고 \(t+1\) 시점의 상태가 \(j\)일 확률.
\(\sum_{k=1}^{N} \xi_{t}(i, k)\): \(t+1\)번째 시점의 상태가 어떤 것이든 관계 없이 \(t\)번째 시점의 상태가 \(i\)일 확률.
\(\sum_{t=1}^{T-1} \sum_{k=1}^{N} \xi_{t}(i, k)\): 시점에 관계 없이 \(i\)번째 상태로 시작할 확률.
\(\sum_{t=1}^{T-1} \xi_{t}(i, j)\): 시점에 관계 없이 \(i\)번째 상태에서 \(j\)번째 상태로 전이할 확률.
5. \(\gamma\)와 방출 확률 \(B\) 계산하기
\(\gamma\)는 방출 확률 \(B\)를 계산하기 위한 기댓값을 구하는 데 쓰인다. 모델 \(\lambda\)와 관측치 시퀀스 \(O\)가 주어졌을 때 \(t\)번째 시점 상태가 \(j\)일 확률이다. \(\gamma\)를 조건부 확률 정의, 즉 \(P(X \mid Y, Z)=P(X, Y \mid Z) / P(Y \mid Z)\)를 활용해 전방/후방 확률 형태로 쓰면 수식11과 같다.
수식11 \(\gamma\) 정의와 전방/후방 확률을 활용한 계산
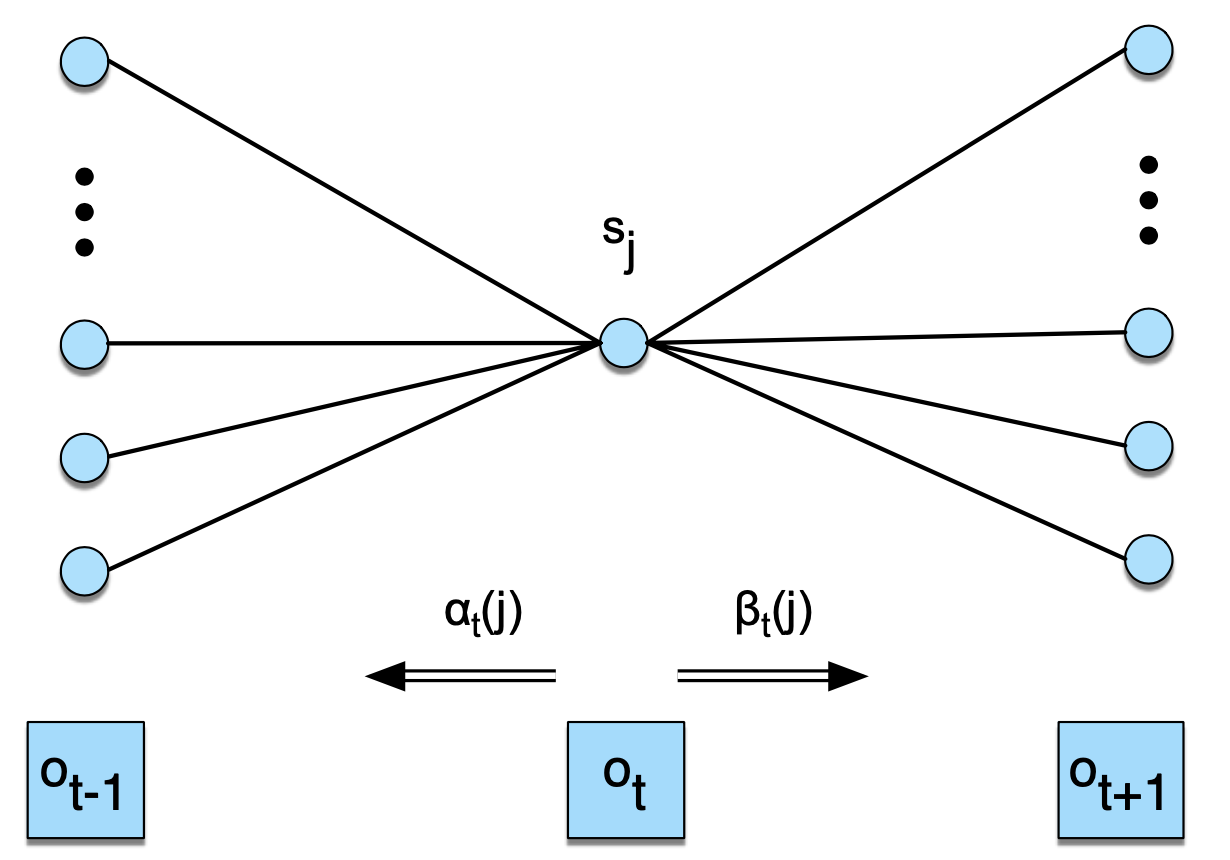
\(\xi\)를 계산할 때 언급했던 것처럼 수식11의 분모는 관측치 시퀀스 \(O\)가 나타날 전체 가능도가 된다. 분자는 관측치 시퀀스 \(O\)가 주어졌을 때 \(t\)번째 시점의 상태가 \(j\)일 가능도를 가리킨다. 수식11의 분자는 그림5와 같이 보면 이해에 도움이 될 것 같다.
그림5 \(\gamma\) 이해하기
방출 확률 추정값을 \(\gamma\)로 기술한 결과는 수식12와 같다. \(\gamma\)로 "관측치 특정 시점이 특정 상태인 기댓값(expected number of times in state j)"을 구하고, 이들 기댓값을 바탕으로 방출 확률을 업데이트한다.
수식12 J번째 상태에서 \(v_{k}\)가 관측될 방출 확률 추정값
6. Expectation-Maximization
히든 마코프 모델(Hidden Markov Model)의 파라미터는 전이 확률(transition probability) \(A\)와 방출 확률(emission probability) \(B\)이다. 지금까지 설명했듯이 우리는 학습 데이터로 관측치(observation)만 가지고 있을 뿐 상태(state)는 알 수 없다.
이 때문에 모든 관측치 각 시점별로 어떤 상태일지 추정하는 과정이 필요하다. 이는 \(\xi\)와 \(\gamma\)로 실현된다. \(\xi\)는 '전이(transition)의 기댓값', \(\gamma\)는 '상태(state)의 기댓값' 계산에 쓰인다. 이렇게 전이와 상태의 기댓값을 모두 알고 있을 경우 전이 확률 \(A\)와 방출 확률 \(B\)를 간단하게 구할 수 있다.
히든 마코프 모델 학습에 사용되는 것이 바로 '바움-웰치 알고리즘'이다. 바움-웰치 알고리즘은 Expectation-Maximization(EM) 알고리즘의 일종이다. 히든 마코프 모델의 학습 개요는 그림6과 같다. 전이 확률 \(A\)와 방출 확률 \(B\)를 랜덤 초기화한다. Expectation 단계에서는 \(A\), \(B\)를 고정시킨 상태에서 전이의 기댓값(\(\xi\)와 연관)과 상태의 기댓값(\(\gamma\)와 연관)을 계산한다. Maximization 단계에서는 \(\xi\)와 \(\gamma\)를 고정한 상태에서 \(A\)와 \(B\)를 업데이트한다.
그림6 히든 마코프 모델의 학습
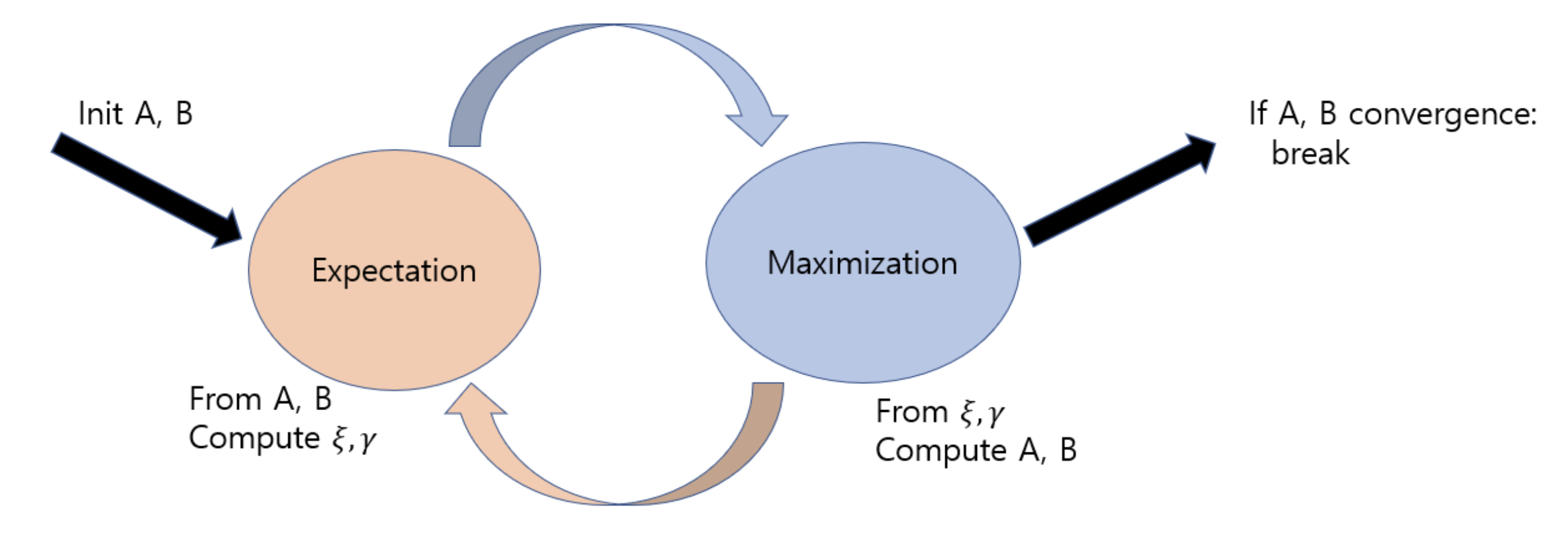
바움-웰치 알고리즘의 의사코드는 그림7과 같다. 바움-웰치 알고리즘에서는 \(A\), \(B\)의 초기값을 어떻게 설정하느냐에 따라 모델의 품질이 확연하게 달라진다고 한다.
그림7 바움-웰치 알고리즘
