1. Legacy Acoustic Model
Info
이번 챕터에서는 히든 마코프 모델(Hidden Markov Model) + 가우시안 믹스처 모델(Gaussian Mixture Model) 조합의 음향 모델(Acoustic Model)을 살펴본다. 이 음향 모델은 딥러닝 기반의 엔드투엔드(end-to-end) 모델들이 등장하기 전 비교적 강력한 성능을 자랑했던 기존 음성 인식 시스템에서 언어모델(Language Model)과 더불어 중요한 역할을 수행했던 컴포넌트이다.
1. Hidden Markov Model
히든 마코프 모델(Hidden Markov Model)에서는 일반적으로 상태 전이에 대한 제약을 두지 않는다. 하지만 히든 마코프 모델을 음성 인식에 적용할 때는 left-to-right 제약을 둔다. 다시 말해 현재 시점 기준으로 이후 상태로 전이만 가능하게 할 뿐, 이전 시점 상태로의 전이는 허용ㅇ하지 않는다는 것이다. 음성 인식을 위한 히든 마코프 모델에서 은닉 상태(hidden state)는 음소(또는 단어)가 될텐데, 음소(또는 단어)는 시간에 대해 불가역적이기 때문에 이렇게 모델링한 것이 아닌가 싶다. 그림1을 보자.
그림1 음성 인식을 위한 HMM 모델링

그림1을 자세히 보면 self-loop를 허용하고 있는 점 역시 눈에 띈다. 화자나 상황에 따라서 특정 음소를 길게 발음할 수도 있고 짧게 말할 수 있는 점을 고려한 모델링이다. 만약 특정 음소를 길게 발음하는 데이터에 대해서는 동일한 은닉 상태를 반복하는 형태로 학습(train)/추론(inference)하게 되는 것이다. 반대로 짧게 발음하는 화자에 대해서는 그 다음 상태(음소)로 전이하도록 한다.
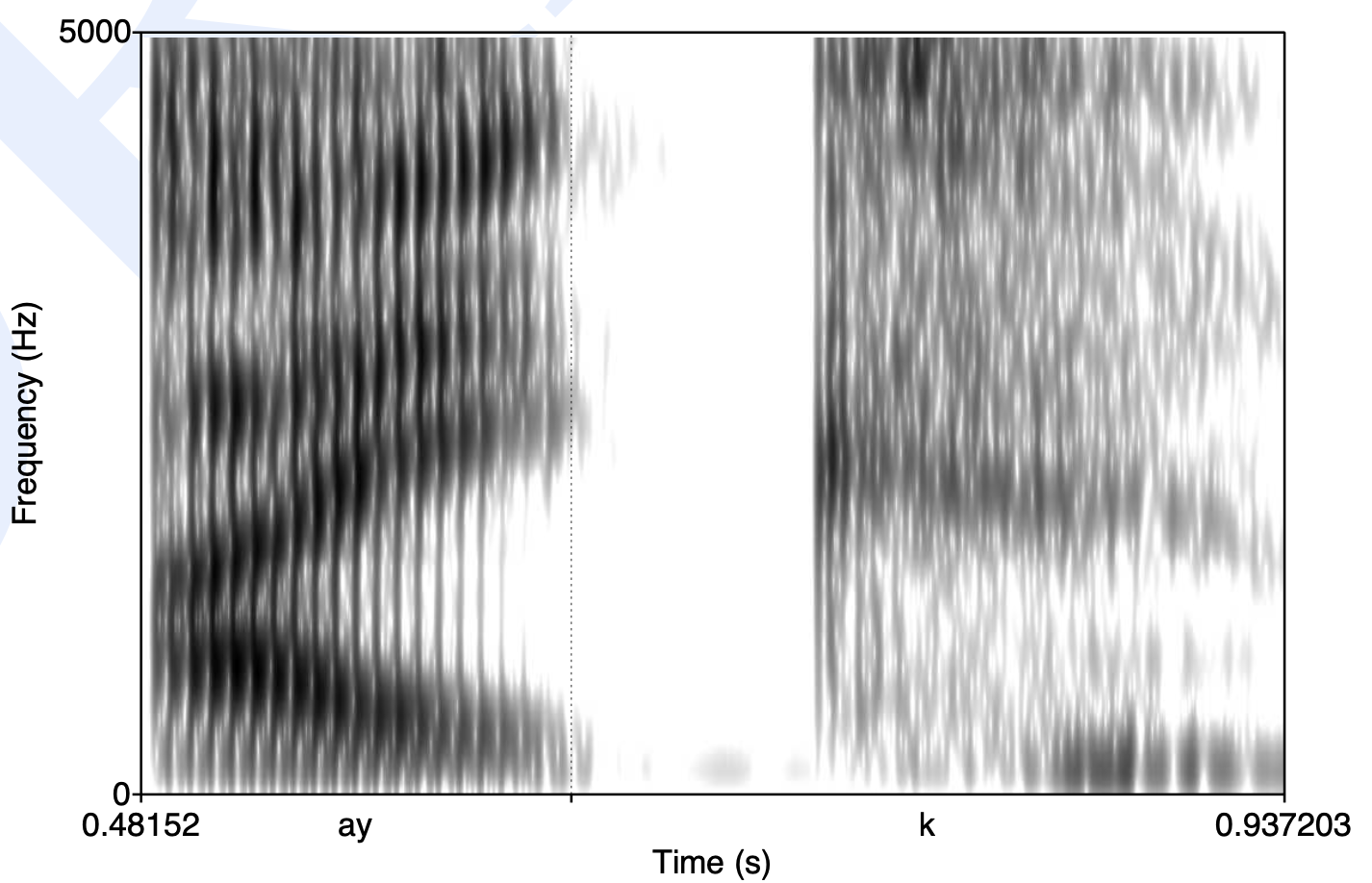
또다른 특이점은 음소를 더 작은 subphone으로 모델링하고 있다는 점이다. 그림1에서는 음소 하나를 3개의 subphone으로 나누었는데, 이는 음소의 음성 패턴과 관계가 있다. 그림2는 영어 모음 [ay, k]의 스펙트로그램을 나타낸다. 'ay'의 경우 동일한 음소인데도 시간 변화에 따라 스펙트로그램이 달라지고 있음을 확인할 수 있다. 'ay'를 하나의 은닉 상태로 모델링하는 것보다는 여러 개로 나누어 모델링하는 것이 음성 인식 성능 향상에 도움이 될 것이다.
그림2 영어 모음 [AY, K]의 스펙트로그램
2. Gaussian Mixture Model
히든 마코프 모델을 음성 인식에 적용하려면 continous 입력에 대한 고려가 필요하다. 그도 그럴 것이 음성 인식의 입력값은 음성 신호가 될텐데, 이 입력값은 히든 마코프 모델 프레임워크에서 관측치(observation) 역할을 한다. 히든 마코프 모델 프레임워크에 사용되는 입력 음성 신호는 MFCCs이다.
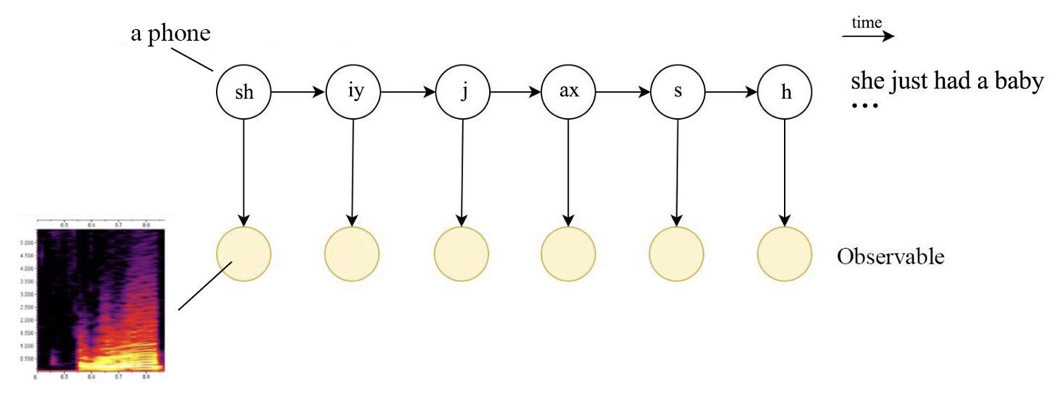
히든 마코프 모델의 주요 컴포넌트는 전이 확률(transition probability)과 방출 확률(emission probability)이다. continous 입력을 고려한다면 이 가운데 방출 확률이 문제가 된다. 예컨대 그림3에서 은닉 상태(음소) 'sh'가 주어졌을 때 해당 관측치(MFCCs)가 나타날 확률, 즉 방출 확률을 구하려면 continous 입력에 확률값을 내어주는 모델(probability model)이 필요하다.
그림3 GAUSSIAN MIXTURE MODEL의 역할
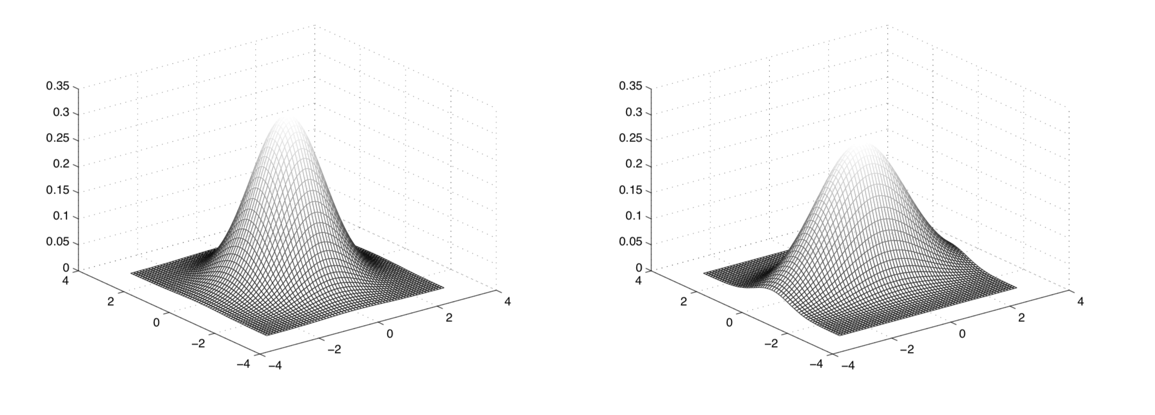
이때 요긴하게 쓰일 수 있는 것이 다변량 가우시안 분포(Multivariate Gaussian Distribution)이다. 정규분포를 다차원 공간에 확장한 분포로 고차원 continous 입력에 대해 확률값을 부여할 수 있다. 가우시안 믹스처 모델(Gaussian Mixture Model)은 한 발 더 나아가 데이터가 여러 개의 정규분포로부터 생성되었다고 가정하는 모델이다. 각 상태(음소)별 MFCC의 분포를 단일 가우시안 모델보다 좀 더 유려하게 모델링할 수 있는 장점이 있다.
음성 인식을 위한 히든 마코프 모델 프레임워크에서 가우시안 믹스처 모델은 히든 마코프 모델과 뗄레야 뗄 수 없는 관계를 가지고 있다. 가우시안 믹스처 모델이 방출 확률을 부여하기 때문이다. 그림4를 두고 예를 들면, 상태(음소)가 'sh'일 때는 그림4의 왼쪽 가우시안 믹스처 모델에, 'k'라면 오른쪽 모델에 입력해 확률값을 계산하는 방식이다. 따라서 음성 인식을 위한 히든 마코프 모델 프레임워크에서 은닉 상태(음소) 개수만큼의 가우시안 믹스처 모델이 필요하게 된다.
그림4 GAUSSIAN MIXTURE MODEL