2. Fourier Transform

Info

푸리에 변환(Fourier Transform)은 시간과 주파수 도메인 관련 함수를 이어주는 수학적인 연산이다. 음성 신호의 스펙트럼 분석 등에 필수적이다. 이 글에서는 컴퓨터 연산에 친화적인 이산 푸리에 변환(Discrete Fourier Transform)을 중심으로 설명하며 직관적인 이해에 중점을 두었다.

1. Discrete Fourier Transform

푸리에 변환(Fourier Transform)이란 시간(time)에 대한 함수(혹은 신호)와 주파수(frequency)에 대한 함수(혹은 신호)를 잇는 수학적인 연산을 가리킨다. 그림1을 보자. 두 개의 단순파(simple wave)가 시간 도메인에서 복합파(complex wave)로 표현되고 있는데, 여기에 푸리에 변환을 실시하면 주파수 도메인에서 두 개의 주파수 성분으로 분해할 수 있다. 반대로 주파수 도메인에 푸리에 변환을 실시하면 시간 도메인에서 복합파를 만들어낼 수 있다.

그림1 FOURIER TRANSFORM

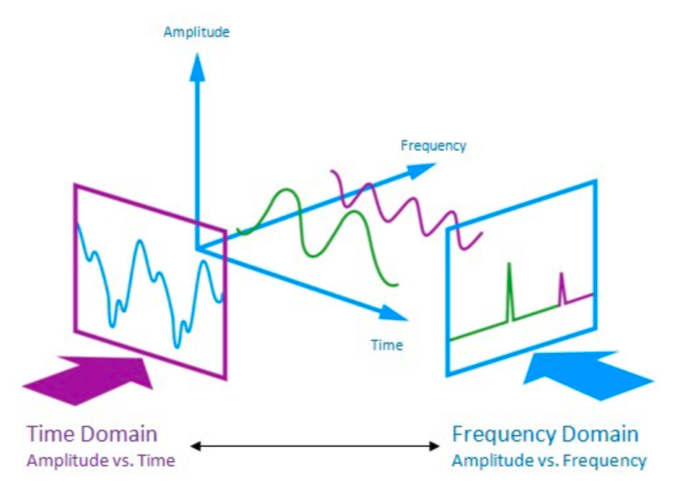
음성 인식에서는 일반적으로 이산 푸리에 변환(Discrete Fourier Transform)이 쓰인다. 컴퓨터는 이산 신호를 처리하는 데 적합하기 때문인데, 이산 푸리에 변환은 특정 도메인(예컨대 시간)의 이산 신호(discrete signal)를 다른 도메인(예컨대 주파수)의 이산 신호로 변환하는 과정이다. 여기에서 이산이란 연속(continuous)과 반대되는 말로써 신호의 값이 연속적이지 않고 띄엄띄엄 있어서 이것들을 제외한 시간이나 주파수에서는 값이 0인 것을 뜻한다. 이 글에서는 이산 푸리에 변환을 중심으로 살펴본다.

이산 푸리에 변환을 식으로 정의한 것은 수식1과 같다. 이산 푸리에 변환을 실시한 뒤 이를 다시 원래 도메인으로 변환하는 과정을 역푸리에 변환(Inverse Fourier Transform)이라고 한다. 이를 이산 신호에 대해 실시한 것이 이산 역푸리에 변환(Inverse Discrete Fourier Transform)이라고 하는데, 수식2와 같다. 자세히 보면 \(e\)의 지수 파트에 음수가 붙어있느냐 아니냐에 따라 푸리에 변환과 역푸리에 변환 사이의 차이가 있음을 확인할 수 있다.

수식1 DISCRETE FOURIER TRANSFORM (1)

\[ X_{k}=\sum_{n=0}^{N-1} x_{n} \cdot e^{-i 2 \pi k n / N} \]

수식2 INVERSE DISCRETE FOURIER TRANSFORM

\[ x_{n}=\frac{1}{N} \sum_{k=0}^{N-1} X_{k} e^{i 2 \pi k n / N} \]

2. Concepts

푸리에 변환을 직관적으로 이해하려면 오일러 공식(Euler's formula)부터 살펴야 한다. 오일러 공식은 수학자 레온하르트 오일러의 이름이 붙은 공식으로, 삼각함수와 지수함수에 대한 관계를 나타낸다. 수식3과 같다(\(i\)는 허수로, 제곱하여 -1이 되는 수). 수식3의 \(\theta\)에 \(\pi\)를 대입하면 \(e^{i \pi}+1=0\)이라는 오일러의 등식을 구할 수 있다.

수식3 EULER'S FORMULA

\[ e^{i \theta}=\cos \theta+i \sin \theta \]

\(e^{i \theta}\)는 복소평면상 반지름이 1인 단위원에 대응한다. 이는 오일러 공식에 의해 실수 파트(real unit, 코사인에 대응)와 허수 파트(imaginary unit, 사인에 대응)의 합으로 표현할 수 있다. 그림2과 같다(그림2에서는 수식3의 \(\theta\)를 \(\varphi\)로 적음).

그림2 EULER'S FORMULA

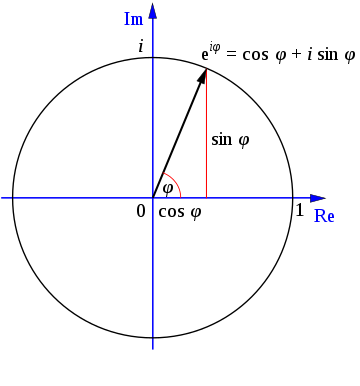
복소 지수 함수는 오일러 공식으로부터 바로 유도할 수 있다. 이 복소 지수 함수는 푸리에 변환의 시작점이 된다. 수식4와 같으며 시각화한 그림은 그림3와 같다. 그림3에서 각각 노란색, 파란색 주기함수에 대응한다.

수식4 복소 지수 함수

\[ \operatorname{cis}(\theta)=e^{i \theta}=\cos \theta+i \sin \theta \]

그림3 복소 지수 함수

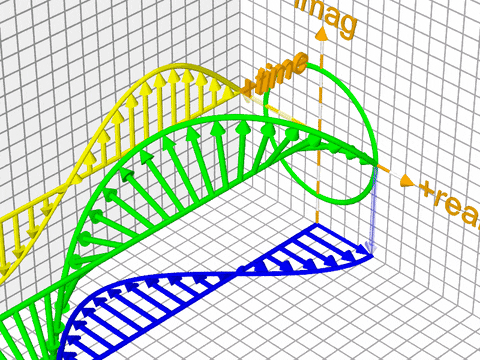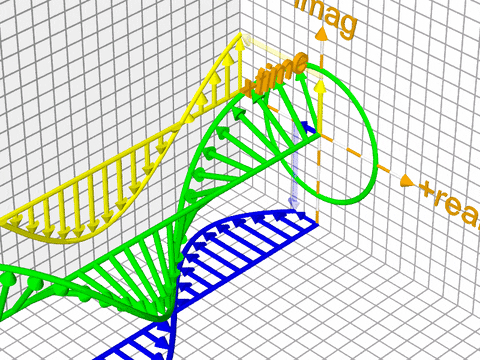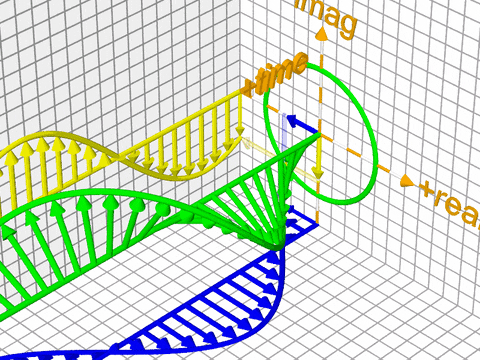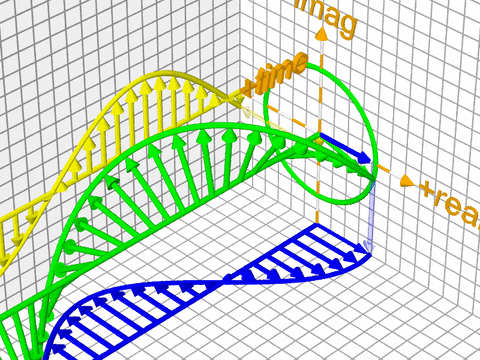
그림4은 푸리에 변환을 개념적으로 나타낸 것이다. 그림3, 그림4을 직관적으로 이해해보기 위해 수식1을 그대로 다시 가져왔다. 시간에서 주파수 도메인으로 푸리에 변환을 실시한다고 했을 때 \(x_{n}\)은 시간 도메인의 \(n\)번째 샘플, \(X_{k}\)는 주파수 도메인의 \(k\)번째 푸리에 변환 결과물이다.

수식1의 첫 번째 줄에서 \(k / N\)은 복소평면상 단위원에서 얼마나 빠른 속도로 회전하는지 나타내는 각 속도(angular velocity)를 가리킨다. \(n\)은 시간 인덱스(time index)를 가리키는데, 시간 인덱스가 1 증가한다고 할 때 각 속도 값이 클수록 그림3의 녹색 실선에 해당하는 움직임이 커지게 된다(단 \(i\), \(2 \pi\)는 상수이기 때문에 복소평면 단위원상 속도에 영향을 미치지 않음).

한편 수식1 두 번째 줄을 보면 푸리에 변환 결과는 복소수(complex number)로, 코사인 함수와 관계 있는 실수부(real part)와 사인 함수와 관계 있는 허수부(imaginary part)로 구성돼 있는 걸 확인할 수 있다.

수식1 DISCRETE FOURIER TRANSFORM (1)

\[ \begin{aligned}X_{k} &=\sum_{n=0}^{N-1} x_{n} \cdot e^{-i 2 \pi k n / N} \\&=\sum_{n=0}^{N-1} x_{n} \cdot\left[\cos \left(\frac{2 \pi}{N} k n\right)-i \cdot \sin \left(\frac{2 \pi}{N} k n\right)\right]\end{aligned} \]

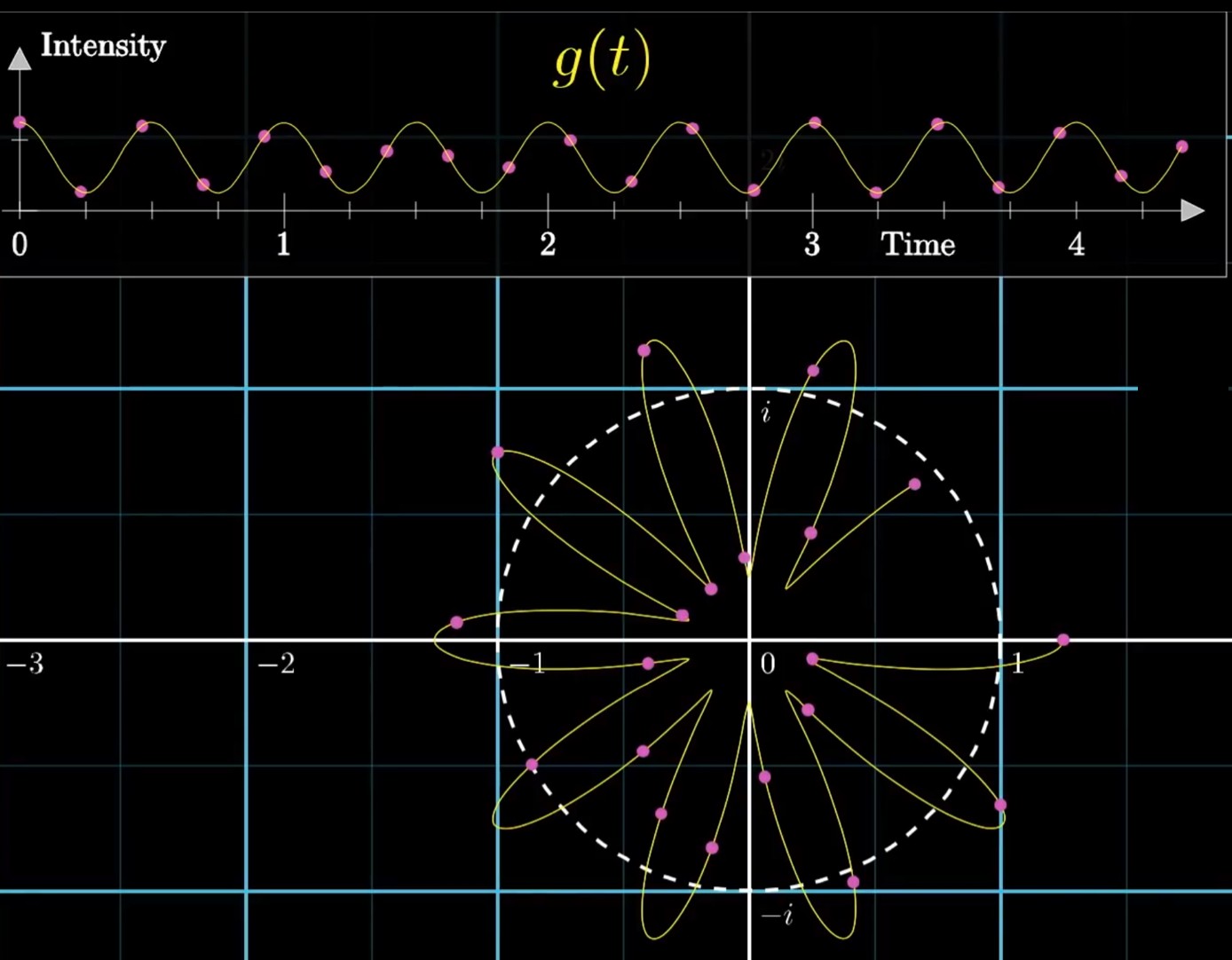
이제 거의 다 왔다. 수식1 이산 푸리에 변환 식을 보면 \(e\) 앞에 시간 도메인의 원래 시그널 \(x_{n}\)이 곱해지는 걸 볼 수 있다. 지수를 포함한 \(e\)항은 복소평면 단위원 위에서 이뤄지는 운동을 의미하는데, 단위원의 반지름은 1이므로 수식1의 시그마 안에 있는 점들의 복소평면상 좌표값은 \(x_{n}\)에 의존적일 것이다.

복소평면상 이들 점들을 모두 더하는 것이 이산 푸리에 변환을 적용한 \(X_{k}\)가 될텐데, 이는 주파수(frequency)가 \(k / N\)일 때 시간 도메인의 원래 신호의 무게 중심이라고 볼 수 있겠다. 따라서 \(X_{k}\)는 시간 도메인 원래 신호에서 \(k / N\)에 해당하는 주파수 성분이라고 볼 수 있다는 것이다.

그림4 FOURIER TRANSFORM 개념도

3. DFT Matrix

이산 푸리에 변환을 matrix form으로 다시 쓰면 수식5와 같다. 여기에서 벡터 \(x\)는 시간 도메인의 원래 신호, 행렬 \(W\)는 수식1 \(e\)항에 대응한다. \(W\)는 \(N \times N\) 크기로 행 인덱스는 \(k\), 열 인덱스는 \(n\)이다. 그림5에서 확인할 수 있듯이 \(W\)의 각 행은 복소평면상 단위원에서 도는 각기 다른 각 속도를 나타낸다. 요컨대 이산 푸리에 변환의 본질은 선형 변환(linear transform)이라는 것이다.

수식5 DISCRETE FOURIER TRANSFORM (2)

\[ \begin{aligned}\vec{X} &=W \cdot \vec{x} \\W_{k n} &=e^{-i 2 \pi k n / N}\end{aligned} \]

그림5 FOURIER TRANSFORM

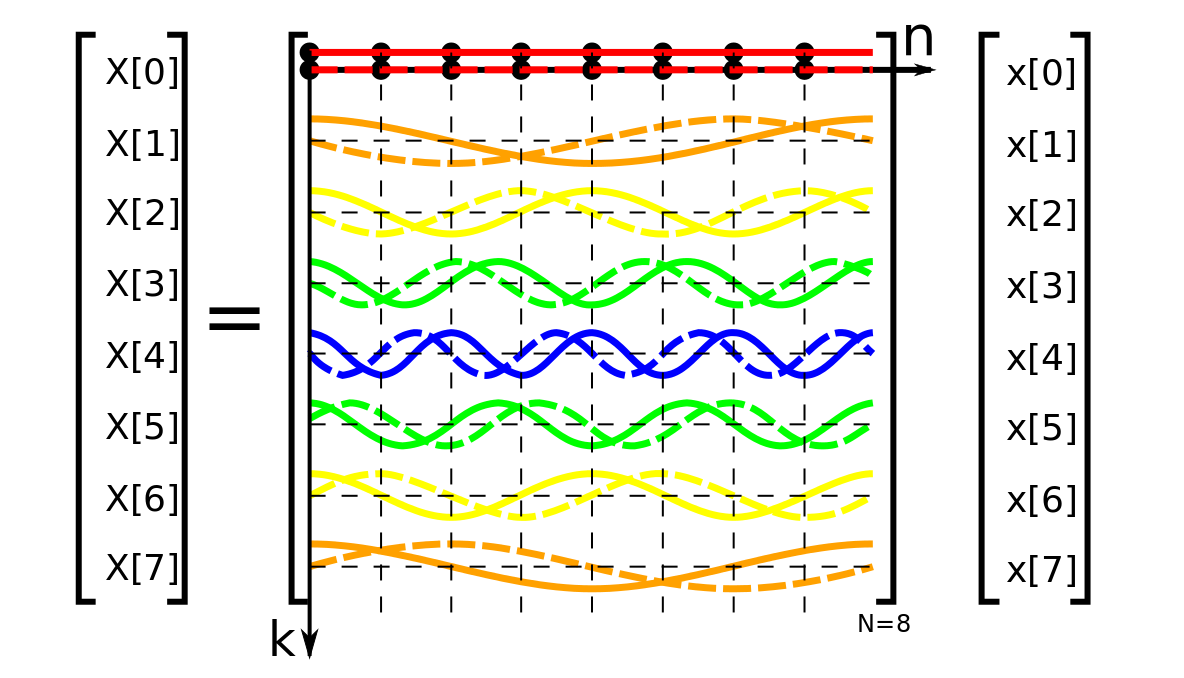
행렬 \(W\)를 DFT 행렬(Discrete Fourier Transform Matrix)이라고도 한다. 그 정의는 수식6과 같다. 단 \(\omega=e^{-2 \pi i / N}\). 수식7은 시간 도메인의 원래 음성 신호가 8개일 때 이산 푸리에 변환을 수행하기 위한 DFT 행렬을 나타낸다. 수식7에서도 알 수 있듯이 DFT 행렬은 켤레 전치가 역행렬(inverse matrix)와 같은 복소수 행렬, 즉 유니터리 행렬(unitary matrix)이다.

수식6 DFT MATRIX

\[ W=\frac{1}{\sqrt{N}}\left[\begin{array}{cccccc}1 & 1 & 1 & 1 & \cdots & 1 \\1 & \omega & \omega^{2} & \omega^{3} & \cdots & \omega^{N-1} \\1 & \omega^{2} & \omega^{4} & \omega^{6} & \cdots & \omega^{2(N-1)} \\1 & \omega^{3} & \omega^{6} & \omega^{9} & \cdots & \omega^{3(N-1)} \\\vdots & \vdots & \vdots & \vdots & \ddots & \vdots \\1 & \omega^{N-1} & \omega^{2(N-1)} & \omega^{3(N-1)} & \cdots & \omega^{(N-1)(N-1)}\end{array}\right] \]

수식7 EIGHT-POINT EXAMPLE

\[ W=\frac{1}{\sqrt{8}}\left[\begin{array}{cccccccc} \omega^0 & \omega^0 & \omega^0 & \omega^0 & \omega^0 & \omega^0 & \omega^0 & \omega^0 \\ \omega^0 & \omega^1 & \omega^2 & \omega^3 & \omega^4 & \omega^5 & \omega^6 & \omega^7 \\ \omega^0 & \omega^2 & \omega^4 & \omega^6 & \omega^8 & \omega^{10} & \omega^{12} & \omega^{14} \\ \omega^0 & \omega^3 & \omega^6 & \omega^9 & \omega^{12} & \omega^{15} & \omega^{18} & \omega^{21} \\ \omega^0 & \omega^4 & \omega^8 & \omega^{12} & \omega^{16} & \omega^{20} & \omega^{24} & \omega^{28} \\ \omega^0 & \omega^5 & \omega^{10} & \omega^{15} & \omega^{20} & \omega^{25} & \omega^{30} & \omega^{35} \\ \omega^0 & \omega^6 & \omega^{12} & \omega^{18} & \omega^{24} & \omega^{30} & \omega^{36} & \omega^{42} \\ \omega^0 & \omega^7 & \omega^{14} & \omega^{21} & \omega^{28} & \omega^{35} & \omega^{42} & \omega^{49} \end{array}\right] \\ =\frac{1}{\sqrt{8}}\left[\begin{array}{cccccccc} 1 & 1 & 1 & 1 & 1 & 1 & 1 & 1 \\ 1 & \omega & -i & -i \omega & -1 & -\omega & i & i \omega \\ 1 & -i & -1 & i & 1 & -i & -1 & i \\ 1 & -i \omega & i & \omega & -1 & i \omega & -i & -\omega \\ 1 & -1 & 1 & -1 & 1 & -1 & 1 & -1 \\ 1 & -\omega & -i & i \omega & -1 & \omega & i & -i \omega \\ 1 & i & -1 & -i & 1 & i & -1 & -i \\ 1 & i \omega & i & -\omega & -1 & -i \omega & -i & \omega \end{array}\right] \]

4. Python Implementation

코드1은 수식5의 파이썬 구현이다. 코드2를 실행하면 numpy에서 제공하는 np.fft.fft 함수와 동일한 결과를 출력하는 걸 확인할 수 있다.

코드1 DISCRETE FOURIER TRANSFORM

import numpy as np

def DFT(x):
    x = np.asarray(x, dtype=float)
    N = x.shape[0]
    n = np.arange(N)
    k = n.reshape((N, 1))
    W = np.exp(-2j * np.pi * k * n / N)

    return np.dot(W, x)

코드2 NUMPY 패키지와의 비교

x = np.random.random(1024)
np.allclose(DFT(x), np.fft.fft(x))

고속 푸리에 변환(Fast Fourier Transform)은 기존 푸리에 변환에서 중복된 계산량을 줄이는 기법이다. 이산 코사인 변환(Discrete Cosine Transform)은 이산 푸리에 변환과 유사하나 복소수 파트를 날리고 실수 파트만을 사용해 효율성을 높였다.

References

https://ratsgo.github.io/speechbook/docs/fe/ft