Skip to content

1. Basic of Least Squares

1. 키워드

  • Inner Product, Dot Product(내적): 동일한 방향에서의 길이의 곱
  • Vector Norm: 벡터의 길이
  • Unit Vector(단위벡터): 길이가 1인 벡터
  • Orthogonal Vectors(직교벡터)


2. Over-determined Linear Systems

Recall a linear system:

\[ \begin{gathered}60 x_{1}+5.5 x_{2}+1 \cdot x_{3}=66 \\65 x_{1}+5.0 x_{2}+0 \cdot x_{3}=74 \\55 x_{1}+6.0 x_{2}+1 \cdot x_{3}=78 \\\vdots \quad \quad \quad \vdots \quad \quad \quad \vdots \quad \quad \quad \vdots\end{gathered} \]

What if we have much more data examples?


Matrix equation:

\[ \left[\begin{array}{ccc}60 & 5.5 & 1 \\65 & 5.0 & 0 \\55 & 6.0 & 1 \\\vdots & \vdots & \vdots\end{array}\right]\left[\begin{array}{l}x_{1} \\x_{2} \\x_{3}\end{array}\right]=\left[\begin{array}{c}66 \\74 \\78 \\\vdots\end{array}\right] \]


\(m \gg n\): more equations than variables → Usually no solution exists.


3. Vector Equation Perspective

Vector equation form:

\[ \left[\begin{array}{c}60 \\65 \\55 \\\vdots\end{array}\right] x_{1}+\left[\begin{array}{c}5.5 \\5.0 \\6.0 \\\vdots\end{array}\right] x_{2}+\left[\begin{array}{l}1 \\0 \\1 \\\vdots\end{array}\right] x_{3}=\left[\begin{array}{c}66 \\74 \\78 \\\vdots\end{array}\right] \]

Compared to the original space \(\mathbb{R}^{n}\), where \(\mathbf{a}_{1}\), \(\mathbf{a}_{2}\), \(\mathbf{a}_{3}\), \(\mathbf{b} \in \mathbb{R}^{n}\), \(\operatorname{Span}\left\{\mathbf{a}_{1}, \mathbf{a}_{2}, \mathbf{a}_{3}\right\}\) will be a thin hyperplane, so it is likely that \(\mathbf{b} \notin\operatorname{Span}\left\{\mathbf{a}_{1}, \mathbf{a}_{2}, \mathbf{a}_{3}\right\}\) → No solution exists.


4. Motivation for Least Squares

Even if no solution exists, we want to approximately obtain the solution for an over-determined system.

Then, how can we define the best approximate solution for our purpose?


5. Inner Product

Given \(\mathbf{u}\), \(\mathbf{v} \in \mathbb{R}^{n}\), we can consider \(\mathbf{u}\) and \(\mathbf{v}\) as \(n \times 1\) matrices.

The transpose \(\mathbf{u}^{T}\) is a \(1 \times n\) matrix, and the matrix product \(\mathbf{u}^{T} \mathbf{v}\) is a \(1 \times 1\) matrix, which we write as a scalar without brackets.

The number \(\mathbf{u}^{T} \mathbf{v}\) is called the inner product or dot product of \(\mathbf{u}\) and \(\mathbf{v}\), and it is written as \(\mathbf{u} \cdot \mathbf{v}\).

For \(\mathbf{u}=\left[\begin{array}{l}3 \\ 2 \\ 1\end{array}\right]\),  \(\mathbf{v}=\left[\begin{array}{l}1 \\ 3 \\ 5\end{array}\right]\), \(\mathbf{u} \cdot \mathbf{v}=\mathbf{u}^{T} \mathbf{v}=\left[\begin{array}{lll}3 & 2 & 1\end{array}\right]\left[\begin{array}{l}1 \\ 3 \\ 5\end{array}\right]=[14]\)


6. Properties of Inner Product

Theorem: Let \(\mathbf{u}\), \(\mathbf{v}\) and \(\mathbf{w}\) be vectors in \(\mathbb{R}^{n}\), and let \(c\) be a scalar.

Then

a) \(\mathbf{u} \cdot \mathbf{v}=\mathbf{v} \cdot \mathbf{u}\)

b) \((\mathbf{u}+\mathbf{v}) \cdot \mathbf{w}=\mathbf{u} \cdot \mathbf{w}+\mathbf{v} \cdot \mathbf{w}\)

c) \((c \mathbf{u}) \cdot \mathbf{v}=c(\mathbf{u} \cdot \mathbf{v})=\mathbf{u} \cdot(c \mathbf{v})\)

d) \(\mathbf{u} \cdot \mathbf{u} \geq \mathbf{0}\), and \(\mathbf{u} \cdot \mathbf{u}=\mathbf{0}\) if and only if \(\mathbf{u}=\mathbf{0}\)


Properties (b) and (c) can be combined to produce the following useful rule:

\[ \left(c_{1} \mathbf{u}_{1}+\cdots+c_{p} \mathbf{u}_{p}\right) \cdot \mathbf{w}=c_{1}\left(\mathbf{u}_{1} \cdot \mathbf{w}\right)+\cdots+c_{p}\left(\mathbf{u}_{p} \cdot \mathbf{w}\right) \]


7. Vector Norm

For \(\mathbf{v} \in \mathbb{R}^{n}\), with entries \(v_{1}, \ldots, v_{n}\), the square root of \(\mathbf{v} \cdot \mathbf{v}\) is defined because \(\mathbf{v} \cdot \mathbf{v}\) is non-negative.

Definition: The length (or norm) of \(\mathbf{v}\) is the non-negative scalar \(\|\mathbf{v}\|\) defined as the square root of \(\mathbf{v} \cdot \mathbf{v}\):

\[ \|\mathbf{v}\|=\sqrt{\mathbf{v} \cdot \mathbf{v}}=\sqrt{v_{1}^{2}+v_{2}^{2}+\cdots+v_{n}^{2}} \text{ and } \|\mathbf{v}\|^{2}=\mathbf{v} \cdot \mathbf{v} \]


8. Geometric Meaning of Vector Norm

Suppose \(\mathbf{v} \in \mathbb{R}^{2}\), say, \(\mathbf{v}=\left[\begin{array}{l}a \\ b\end{array}\right]\).

\(\|\mathbf{v}\|\) is the length of the line segment from the origin to \(\mathbf{v}\).

This follows from Pythagorean Theorem applied to a triangle such as the one shown in the following figure:


001


For any scalar \(c\), the length \(c \mathbf{v}\) is \(|c|\) times the length of \(\mathbf{v}\), that is, \(\|c \mathbf{v}\|=|c|\|\mathbf{v}\|\).


9. Unit Vector

A vector whose length is \(1\) is called a unit vector.

Normalizing a vector: Given a nonzero vector \(\mathbf{v}\), if we divide it by its length, we obtain a unit vector \(\mathbf{u}=\frac{1}{\|\mathbf{v}\|} \mathbf{v}\).

\(\mathbf{u}\) is in the same direction as \(\mathbf{v}\), but its length is \(1\).


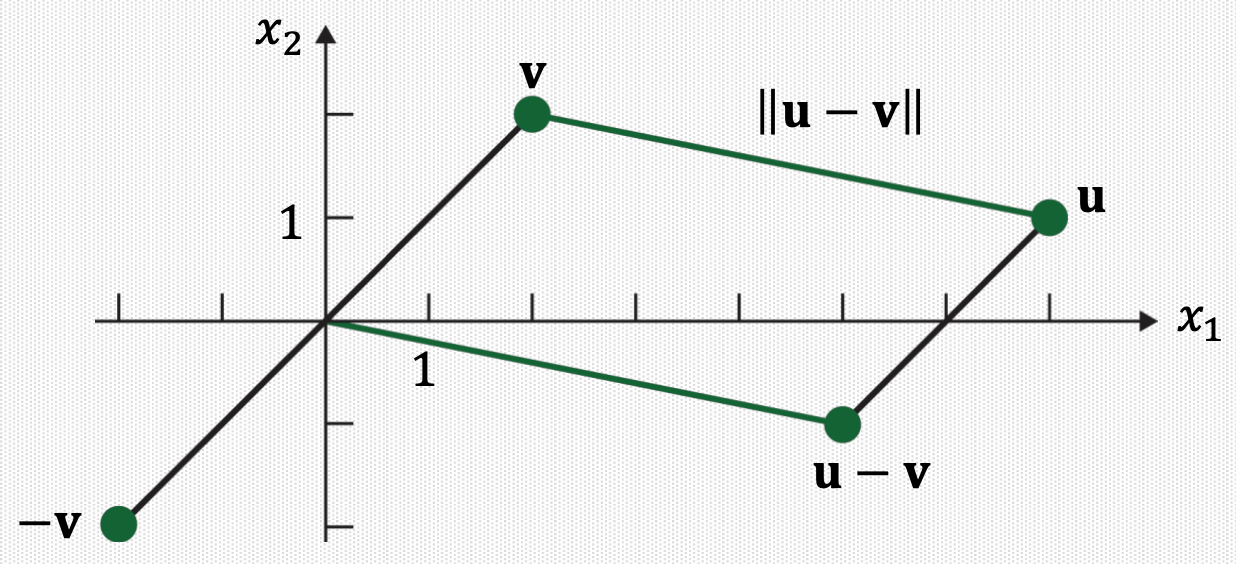
10. Distance between Vectors in \(\mathbb{R}^{n}\)

Definition: For \(\mathbf{u}\) and \(\mathbf{v}\) in \(\mathbb{R}^{n}\), the distance between \(\mathbf{u}\) and \(\mathbf{v}\), written as dist \((\mathbf{u}, \mathbf{v})\), is the length of the vector \(\mathbf{u}-\mathbf{v}\), that is, dist \((\mathbf{u}, \mathbf{v})=\|\mathbf{u}-\mathbf{v}\|\).


Example

\[ \text{Compute the distance between the vector: } \mathbf{u}=\left[\begin{array}{l}6 \\1\end{array}\right] \text { and } \mathbf{v}=\left[\begin{array}{l}3 \\2\end{array}\right]\text{.} \]
\[ \text{Calculate: }\begin{aligned}&\mathbf{u}-\mathbf{v}=\left[\begin{array}{l}6 \\1\end{array}\right]-\left[\begin{array}{l}3 \\2\end{array}\right]=\left[\begin{array}{c}3 \\-1\end{array}\right] \\&\|\mathbf{u}-\mathbf{v}\|=\sqrt{3^{2}+(-1)^{2}}=\sqrt{10}\end{aligned} \]


The distance from \(\mathbf{u}\) to \(\mathbf{v}\) is the same as the distance from \(\mathbf{u}-\mathbf{v}\) to \(0\).


002


11. Inner Product and Angle Between Vectors

Inner product between \(\mathbf{u}\) and \(\mathbf{v}\) can be rewritten using their norms and angle:

\[ \mathbf{u} \cdot \mathbf{v}=\|\mathbf{u}\|\|\mathbf{v}\| \cos \theta \]


Example

003

\[ \mathbf{u} \cdot \mathbf{v}=\left[\begin{array}{l}2 \\ 1\end{array}\right] \cdot\left[\begin{array}{l}1 \\ 3\end{array}\right]=\left[\begin{array}{ll}2 & 1\end{array}\right]\left[\begin{array}{l}1 \\ 3\end{array}\right]=5 \]
\[ \|\mathbf{u}\|=\sqrt{2^{2}+1^{2}}=\sqrt{5} \quad\|\mathbf{v}\|=\sqrt{1^{2}+3^{2}}=\sqrt{10} \]
\[ \mathbf{u} \cdot \mathbf{v}=5=\|\mathbf{u}\|\|\mathbf{v}\| \cos \theta=\sqrt{5} \cdot \sqrt{10} \cos \theta \]
\[ \Rightarrow \cos \theta=\frac{5}{\sqrt{50}}=\frac{1}{\sqrt{2}} \]
\[ \Rightarrow \theta=45^{\circ} \]


12. Orthogonal Vectors

Definition: \(\mathbf{u} \in \mathbb{R}^{n}\) and \(\mathbf{v} \in \mathbb{R}^{n}\) are orthogonal (to each other) if \(\mathbf{u} \cdot \mathbf{v}=0\), that is, \(\mathbf{u} \cdot \mathbf{v}=\|\mathbf{u}\|\|\mathbf{v}\| \cos \theta=0\).


004


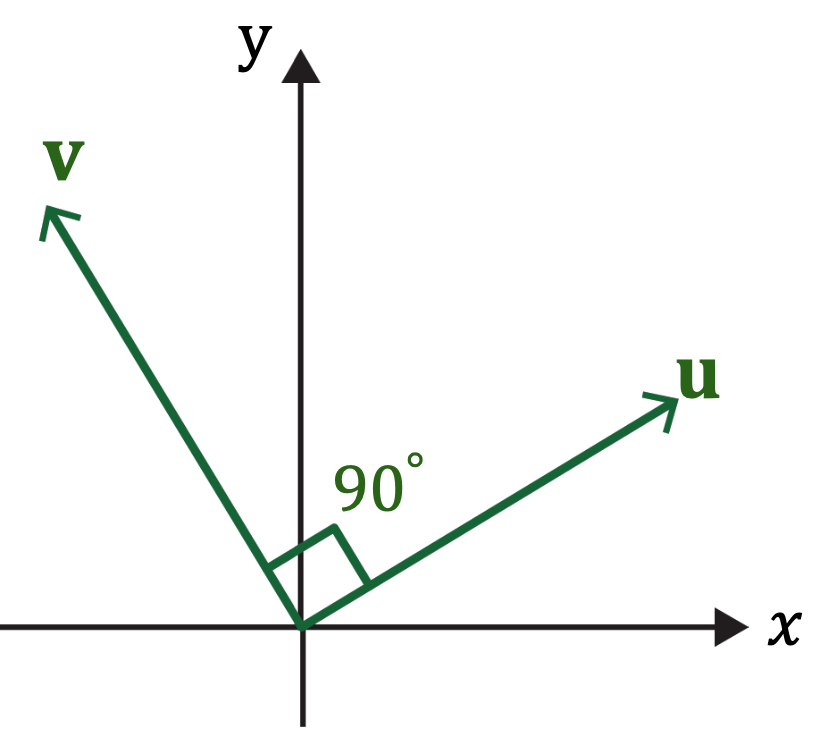
→ \(\mathbf{u} \cdot \mathbf{v} {c o s} \theta=0\) for nonzero vectors \(\mathbf{u}\) and \(\mathbf{v}\)

→ \(\theta=90^{\circ}(\mathbf{u} \perp \mathbf{v})\)

→ \(\mathbf{u}\) and \(\mathbf{v}\) are perpendicular each other.


13. Back to Over-Determined System

Let's start with the original problem:

\[ \left[\begin{array}{lll}60 & 5.5 & 1 \\65 & 5.0 & 0 \\55 & 6.0 & 1\end{array}\right]\left[\begin{array}{l}x_{1} \\x_{2} \\x_{3}\end{array}\right]=\left[\begin{array}{l}66 \\74 \\78\end{array}\right] \]

Using the inverse matrix, the solution is \(\mathbf{x}=\left[\begin{array}{c}-0.4 \\ 20 \\ -20\end{array}\right]\)


Let's add one more example:

\[ \left[\begin{array}{lll}60 & 5.5 & 1 \\65 & 5.0 & 0 \\55 & 6.0 & 1 \\50 & 5.0 & 0\end{array}\right]\left[\begin{array}{l}x_{1} \\x_{2} \\x_{3}\end{array}\right]=\left[\begin{array}{l}66 \\74 \\78 \\72\end{array}\right] \]

Now, let's use the previous solution \(\mathbf{x}={\left[\begin{array}{c}-0.4 \\ 20 \\ -20\end{array}\right]}\)

\(\left[\begin{array}{ccc}60 & 5.5 & 1 \\65 & 5.0 & 0 \\55 & 6.0 & 1 \\50 & 5.0 & 1\end{array}\right]{\left[\begin{array}{c}-0.4 \\20 \\-20\end{array}\right]}=\left[\begin{array}{l}66 \\74 \\78 \\{60}\end{array}\right] \neq\left[\begin{array}{l}66 \\74 \\78 \\{72}\end{array}\right] \quad \begin{gathered}\text { Errors } \\0 \\0 \\0 \\{12}\end{gathered}\)


How about using slightly different solution \(\mathbf{x}={\left[\begin{array}{c}-0.12 \\16 \\-9.5\end{array}\right]}\)?

\(\left[\begin{array}{ccc}60 & 5.5 & 1 \\65 & 5.0 & 0 \\55 & 6.0 & 1 \\50 & 5.0 & 1\end{array}\right]{\left[\begin{array}{c}-0.12 \\16 \\-9.5\end{array}\right]}=\left[\begin{array}{l}{71.3} \\{72.2} \\{79.9} \\{64.5}\end{array}\right] \neq\left[\begin{array}{l}{66} \\{74} \\{78} \\{72}\end{array}\right] \quad \begin{gathered}\text { Errors } \\{-5.3} \\{1.8} \\{-1.9} \\{7.5}\end{gathered}\)


14. Which One is Better Solution?

\(\left[\begin{array}{ccc}60 & 5.5 & 1 \\65 & 5.0 & 0 \\55 & 6.0 & 1 \\50 & 5.0 & 1\end{array}\right]{\left[\begin{array}{c}-0.12 \\16 \\-9.5\end{array}\right]}=\left[\begin{array}{l}{71.3} \\{72.2} \\{79.9} \\{64.5}\end{array}\right] \neq\left[\begin{array}{l}{66} \\{74} \\{78} \\{72}\end{array}\right] \quad \begin{gathered}\text { Errors } \\{-5.3} \\{1.8} \\{-1.9} \\{7.5}\end{gathered}\)\(\left[\begin{array}{ccc}60 & 5.5 & 1 \\65 & 5.0 & 0 \\55 & 6.0 & 1 \\50 & 5.0 & 1\end{array}\right]{\left[\begin{array}{c}-0.4 \\20 \\-20\end{array}\right]}\ \ =\left[\begin{array}{l}66 \\74 \\78 \\{60}\end{array}\right] \neq\left[\begin{array}{l}66 \\74 \\78 \\{72}\end{array}\right] \quad \begin{gathered}\ \ \ \text { Errors } \\0 \\0 \\0 \\{12}\end{gathered}\)


15. Least Squares: Best Approximation Criterion

Let's use the squared sum of errors:

\(\left[\begin{array}{ccc}60 & 5.5 & 1 \\65 & 5.0 & 0 \\55 & 6.0 & 1 \\50 & 5.0 & 1\end{array}\right]{\left[\begin{array}{c}-0.12 \\16 \\-9.5\end{array}\right]}=\left[\begin{array}{l}{71.3} \\{72.2} \\{79.9} \\{64.5}\end{array}\right] \neq\left[\begin{array}{l}{66} \\{74} \\{78} \\{72}\end{array}\right] \begin{gathered}\text { Errors } \\{-5.3} \\{1.8} \\{-1.9} \\{7.5}\end{gathered}\begin{gathered}\text{Sum of squared errors}\\\left({(-5.3)^{2}+1.8^{2}+(-1.9)^{2}+7.5^{2}}\right)^{0.5} \\=9.55\end{gathered}\)

\(\left[\begin{array}{ccc}60 & 5.5 & 1 \\65 & 5.0 & 0 \\55 & 6.0 & 1 \\50 & 5.0 & 1\end{array}\right]{\left[\begin{array}{c}-0.4 \\20 \\-20\end{array}\right]} =\left[\begin{array}{l}66 \\74 \\78 \\{60}\end{array}\right] \neq\left[\begin{array}{l}66 \\74 \\78 \\{72}\end{array}\right] \begin{gathered}\text { Errors } \\0 \\0 \\0 \\{12}\end{gathered}\begin{gathered}\text{Sum of squared errors}\\\left(0^{2}+0^{2}+0^{2}+{(-12)^{2}}\right)^{0.5} \\=12\end{gathered}\)


16. Least Squares Problem

Now, the sum of squared errors can be represented as \(\|\mathbf{b}-A \mathbf{x}\|\).

Definition: Given an overdetermined system \(A \mathbf{x} \simeq \mathbf{b}\) where \(A \in \mathbb{R}^{m \times n}\), \(\mathbf{b} \in \mathbb{R}^{n}\), and \(m \gg n\), a least squares solution \(\hat{\mathbf{x}}\) is defined as \(\widehat{\mathbf{x}}=\arg \min _{\mathbf{x}}\|\mathbf{b}-A \mathbf{x}\|\)

The most important aspect of the least squares problem is that no matter what \(\mathbf{x}\) we select, the vector \(A \mathbf{x}\) will necessarily be in the column space \(\operatorname{Col}A\).

Thus, we seek for \(\mathbf{x}\) that makes \(A \mathbf{x}\) as the closest point in \(\operatorname{Col}A\) to \(\mathbf{b}\).

References