7. Surjective and Injective
1. 키워드
- Onto, Surjective(전사함수): 공역과 치역이 같은 함수
- One-to-one, Injective(일대일함수): 정의역의 서로 다른 원소를 공역의 서로 다른 원소로 대응시키는 함수
2. ONTO and ONE-TO-ONE
Definition: A mapping \(T: \mathbb{R}^{n} \rightarrow \mathbb{R}^{m}\) is said to be onto \(\mathbb{R}^{m}\) if each \(\mathbf{b} \in \mathbb{R}^{m}\) is the image of at least one \(\mathbf{x} \in \mathbb{R}^{n}\). That is, the range is equal to the co-domain.

Definition: A mapping \(T: \mathbb{R}^{n} \rightarrow \mathbb{R}^{m}\) is said to be one-to-one if each \(\mathbf{b} \in \mathbb{R}^{m}\) is the image of at most one \(\mathbf{x} \in \mathbb{R}^{n}\). That is, each output vector in the range is mapped by only one input vector, no more than that.
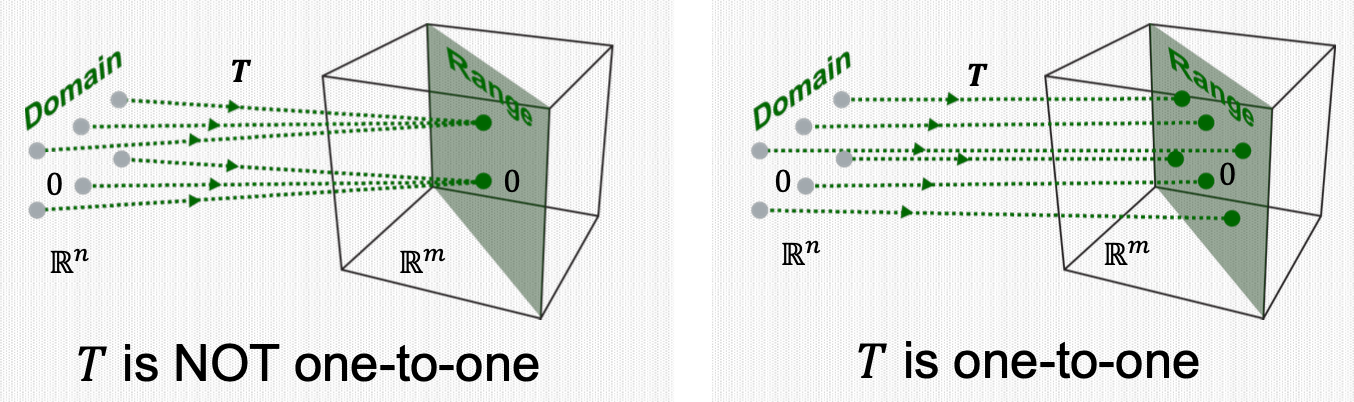
Let \(T: \mathbb{R}^{n} \rightarrow \mathbb{R}^{m}\) be a linear transformation, i.e., \(T(\mathbf{x})=A \mathbf{x} \text { for all } \mathbf{x} \in \mathbb{R}^{n}\).
\(T\) is one-to-one if and only if the columns of \(A\) are linearly independent.
\(T\) maps \(\mathbb{R}^{n}\) onto \(\mathbb{R}^{m}\) if and only if the columns of \(A\) span \(\mathbb{R}^{m}\).