5. Basis and Dimension of Subspace

1. 키워드

Subspace(부분 공간): 선형결합에 닫혀 있는 부분 집합
Basis(기저): Fully span하며 선형 독립을 만족하는 벡터 집합
Dimension(차원): Basis의 개수
Rank(계수): Column space의 차원

2. Span and Subspace

Definition: A subspace \(H\) is defined as a subset of \(\mathbb{R}^{n}\) closed under linear combination:

For any two vectors, \(\mathbf{u}_{1}\), \(\mathbf{u}_{2} \in H\), and any two scalars \(c\) and \(d\), \(c \mathbf{u}_{1}+d \mathbf{u}_{2} \in H\).

\(\operatorname{Span}\left\{\mathbf{v}_{1}, \cdots, \mathbf{v}_{p}\right\}\) is always a subspace, why?

\(\mathbf{u}_{1}=a_{1} \mathbf{v}_{1}+\cdots+a_{p} \mathbf{v}_{p}, \mathbf{u}_{2}=b_{1} \mathbf{v}_{1}+\cdots+b_{p} \mathbf{v}_{p}\)
\(c \mathbf{u}_{1}+d \mathbf{u}_{2}=c\left(a_{1} \mathbf{v}_{1}+\cdots+a_{p} \mathbf{v}_{p}\right)+d\left(b_{1} \mathbf{v}_{1}+\cdots+b_{p} \mathbf{v}_{p}\right)=\left(c a_{1}+d b_{1}\right) \mathbf{v}_{1}+\cdots+\left(c a_{p}+d b_{p}\right) \mathbf{v}_{p}\)

In fact, a subspace is always represented as \(\operatorname{Span}\left\{\mathbf{v}_{1}, \cdots, \mathbf{v}_{p}\right\}\).

3. Basis of a Subspace

Definition: A basis of a subspace \(H\) is a set of vectors that satisfies both of the following:

Fully spans the given subspace \(H\)
Linearly independent (i.e., no redundancy)

In the previous example, where \(H =\operatorname{Span}\left\{\mathbf{v}_{1}, \mathbf{v}_{2}, \mathbf{v}_{3}\right\}\), \(\operatorname{Span}\left\{\mathbf{v}_{1}, \mathbf{v}_{2}\right\}\) forms a plane, but \(\mathbf{v}_{3}=2 \mathbf{v}_{1}+3 \mathbf{v}_{2} \in\operatorname{Span}\left\{\mathbf{v}_{1}, \mathbf{v}_{2}\right\}\), \(\left\{\mathbf{v}_{1}, \mathbf{v}_{2}\right\}\) is a basis of \(H\), but not \(\left\{\mathbf{v}_{1}, \mathbf{v}_{2}, \mathbf{v}_{3}\right\}\) nor \(\left\{\mathbf{v}_{1}\right\}\) is a basis.

4. Non-Uniqueness of Basis

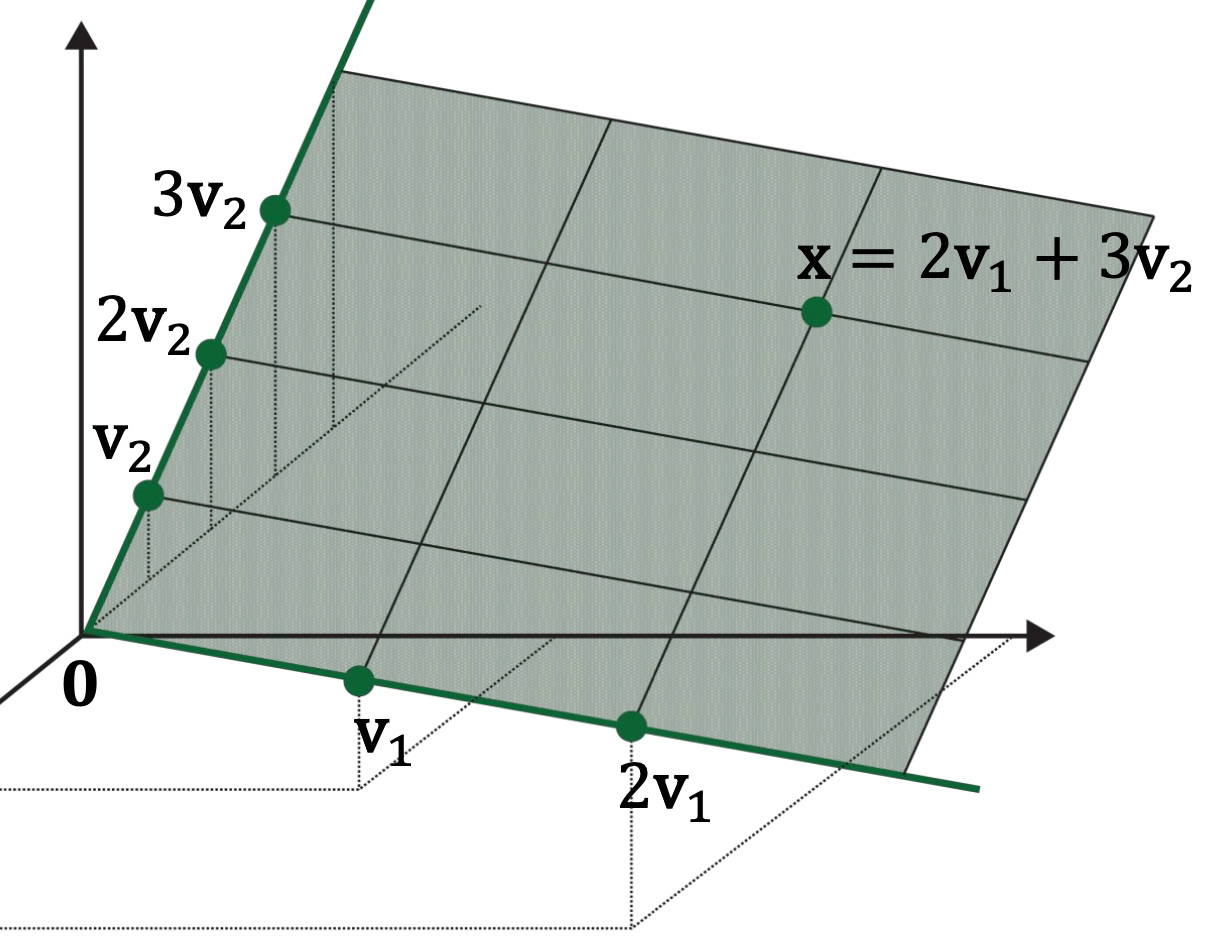
Consider a subspace \(H\) (green plane).

Is a basis unique?

That is, is there any other set of linearly independent vectors that span the same subspace \(H\)?

5. Dimension of Subspace

What is then unique, given a particular subspace \(H\)?

Even though different bases exist for \(H\), the number of vectors in any basis for \(H\) will be unique.

We call this number as the dimension of \(H\), denoted as dim \(H\).

In the previous example, the dimension of the plane is \(2\), meaning any basis for this subspace contains exactly two vectors.

6. Column Space of Matrix

Definition: The column space of a matrix \(A\) is the subspace spanned by the columns of \(A\). We call the column space of \(A\) as \(\operatorname{Col}A\).

\(A=\left[\begin{array}{ll}1 & 1 \\1 & 0 \\0 & 1\end{array}\right]\) → \(\operatorname{Col}A=\operatorname{Span}\left\{\left[\begin{array}{l}1 \\1 \\0\end{array}\right],\left[\begin{array}{l}1 \\0 \\1\end{array}\right]\right\}\)

What is dim \(\operatorname{Col}A\)?

7. Matrix with Linearly Dependent Columns

Given \(A=\left[\begin{array}{lll}1 & 1 & 2 \\ 1 & 0 & 1 \\ 0 & 1 & 1\end{array}\right]\), note that \(\left[\begin{array}{l}2 \\ 1 \\ 1\end{array}\right]=\left[\begin{array}{l}1 \\ 1 \\ 0\end{array}\right]+\left[\begin{array}{l}1 \\ 0 \\ 1\end{array}\right]\), i.e., the third column is a linear combination of the first two.

\(\operatorname{Col}A=\operatorname{Span}\left\{\left[\begin{array}{l}1 \\ 1 \\ 0\end{array}\right],\left[\begin{array}{l}1 \\ 0 \\ 1\end{array}\right],\left[\begin{array}{l}2 \\ 1 \\ 1\end{array}\right]\right\}\) → \(\operatorname{Col}A=\operatorname{Span}\left\{\left[\begin{array}{l}1 \\ 1 \\ 0\end{array}\right],\left[\begin{array}{l}1 \\ 0 \\ 1\end{array}\right]\right\}\)