4. Linear Independence/Dependence
1. 키워드
- Linear Independence(선형독립): 벡터 집합의 어떠한 벡터도 나머지 벡터들의 선형결합으로 나타낼 수 없음
- Linear Dependence(선형종속): 벡터 집합의 벡터 중 적어도 하나는 나머지 벡터들의 선형결합으로 나타낼 수 있음
2. Recall: Linear System
| Person ID | Weight | Height | Is_smoking | Life-span |
|---|---|---|---|---|
| 1 | 60kg | 5.5ft | Yes (=1) | 66 |
| 2 | 65kg | 5.0ft | No (=0) | 74 |
| 3 | 55kg | 6.0ft | Yes (=1) | 78 |
Recall the matrix equation of a linear system:
Or, a vector equation is written as:
3. Uniqueness of Solution for \(A \mathbf{x}=\mathbf{b}\)
The solution exists only when \(\mathbf{b} \in \operatorname{Span}\left\{\mathbf{a}_{1}, \mathbf{a}_{2}, \mathbf{a}_{3}\right\}\).
\(\begin{gathered} {\left[\begin{array}{l} 60 \\ 65 \\ 55 \end{array}\right] x_{1}+\left[\begin{array}{l} 5.5 \\ 5.0 \\ 6.0 \end{array}\right] x_{2}+\left[\begin{array}{l} 1 \\ 0 \\ 1 \end{array}\right] x_{3}=\left[\begin{array}{l} 66 \\ 74 \\ 78 \end{array}\right]} \\ \mathbf{a}_{1} x_{1}+\mathbf{a}_{2} x_{2}+\mathbf{a}_{3} x_{3}=\mathbf{b} \end{gathered}\)
If the solution exists for \(A \mathbf{x}=\mathbf{b}\), when is it unique?
It is unique when \(\mathbf{a}_{1}\), \(\mathbf{a}_{2}\), and \(\mathbf{a}_{3}\) are linearly independent.
Infinitely many solutions exist when \(\mathbf{a}_{1}\), \(\mathbf{a}_{2}\), and \(\mathbf{a}_{3}\) are linearly dependent.
4. Linear Independence
(Practical) Definition:
Given a set of vectors \(\mathbf{v}_{1}, \cdots, \mathbf{v}_{p} \in \mathbb{R}^{n}\), check if \(\mathbf{v}_{j}\) can be represented as a linear combination of the previous vectors \(\left\{\mathbf{v}_{1}, \mathbf{v}_{2}, \ldots, \mathbf{v}_{j-1}\right\}\) for \(j=1, \ldots, p\), e.g., \(\mathbf{v}_{j} \in \operatorname{Span}\left\{\mathbf{v}_{1}, \mathbf{v}_{2}, \ldots, \mathbf{v}_{j-1}\right\}\) for some \(j=1, \ldots, p\)?
If at least one such \(\mathbf{v}_{j}\) is found, then \(\left\{\mathbf{v}_{1}, \cdots, \mathbf{v}_{p}\right\}\) is linearly dependent.
If no such \(\mathbf{v}_{j}\) is found, then \(\left\{\mathbf{v}_{1}, \cdots, \mathbf{v}_{p}\right\}\) is linearly independent.
(Formal) Definition:
Consider \(x_{1} \mathbf{v}_{1}+x_{2} \mathbf{v}_{2} \cdots+x_{p} \mathbf{v}_{p}=\mathbf{0}\).
Obviously, one solution is \(\mathbf{x}=\left[\begin{array}{c}x_{1} \\ x_{2} \\ \vdots \\ x_{p}\end{array}\right]=\left[\begin{array}{c}0 \\ 0 \\ \vdots \\ 0\end{array}\right]\), which we call a trivial solution.
\(\mathbf{v}_{1}, \cdots, \mathbf{v}_{p}\) are linearly independent if this is the only solution.
\(\mathbf{v}_{1}, \cdots, \mathbf{v}_{p}\) are linearly dependent if this system also has other nontrivial solutions, e.g., at least one \(x_{i}\) being nonzero.
5. Two Definitions are Equivalent
If \(\mathbf{v}_{1}, \cdots, \mathbf{v}_{p}\) are linearly dependent, consider a nontrivial solution.
In the solution, let's denote \(j\) as the last index such that \(x_{j} \neq 0\).
Then one can write \(x_{j} \mathbf{v}_{j}=-x_{1} \mathbf{v}_{1}-\cdots-x_{j-1} \mathbf{v}_{j-1}\), and safely divide it by \(x_{j}\), resulting in \(\mathbf{v}_{j}=-\frac{x_{1}}{x_{j}} \mathbf{v}_{1}-\cdots-\frac{x_{j-1}}{x_{j}} \mathbf{v}_{j-1} \in\operatorname{Span}\left\{\mathbf{v}_{1}, \mathbf{v}_{2}, \ldots, \mathbf{v}_{j-1}\right\}\) which means \(\mathbf{v}_{j}\)can be represented as a linear combination of the previous vectors.
6. Geometric Understanding of Linear Dependence
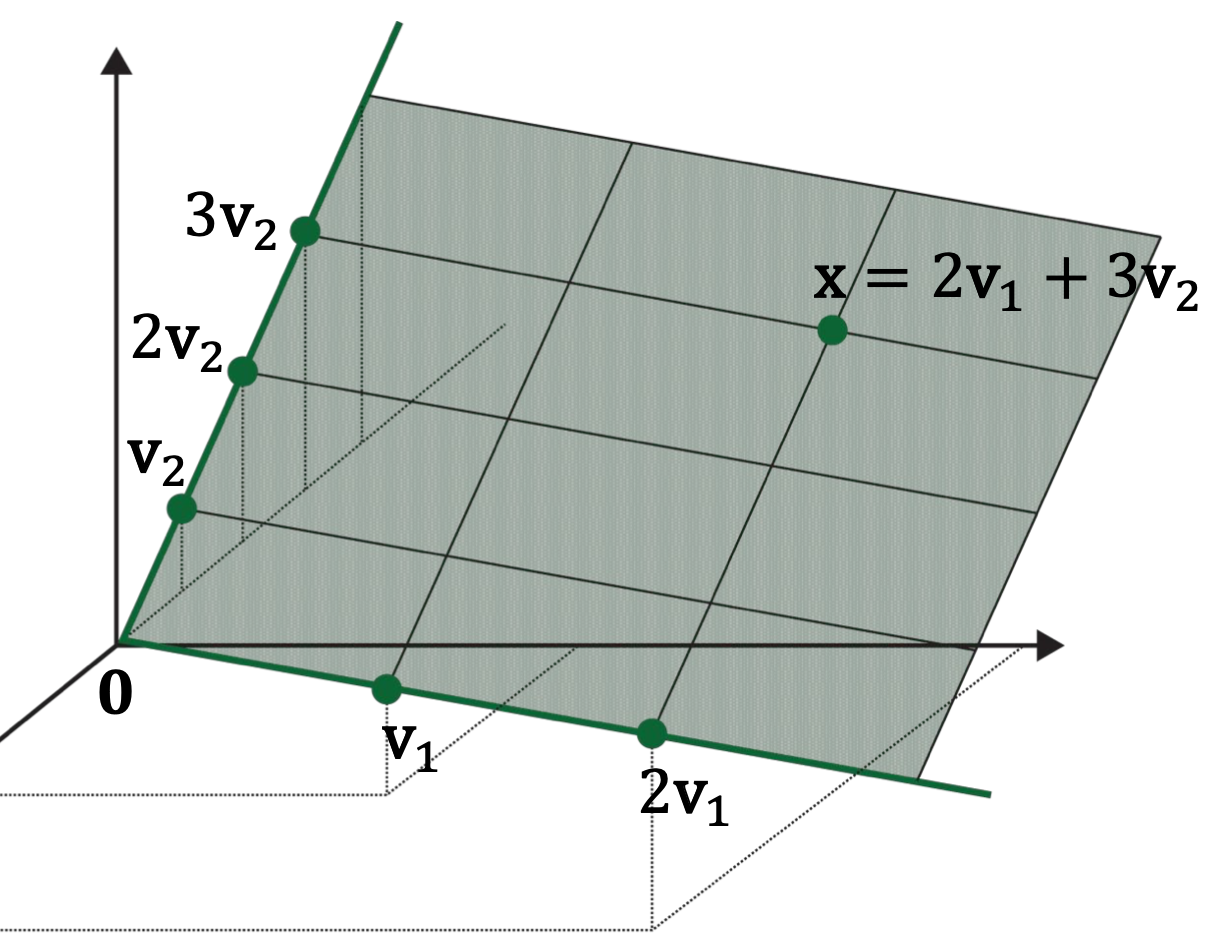
Given two vectors \(\mathbf{v}_{1}\) and \(\mathbf{v}_{2}\), Suppose \(\operatorname{Span}\left\{\mathbf{v}_{1}, \mathbf{v}_{2}\right\}\) is the plane on the right.
When is the third vector \(\mathbf{v}_{3}\) linearly dependent of \(\mathbf{v}_{1}\) and \(\mathbf{v}_{2}\)?
That is, \(\mathbf{v}_{3} \in \operatorname{Span}\left\{\mathbf{v}_{1}, \mathbf{v}_{2}\right\}\) ?
7. Linear Dependence
A linearly dependent vector does not increase Span!
If \(\mathbf{v}_{3} \in \operatorname{Span}\left\{\mathbf{v}_{1}, \mathbf{v}_{2}\right\}\) , then \(\operatorname{Span}\left\{\mathbf{v}_{1}, \mathbf{v}_{2}\right\}=\operatorname{Span}\left\{\mathbf{v}_{1}, \mathbf{v}_{2}, \mathbf{v}_{3}\right\}\), why?
Suppose \(\mathbf{v}_{3}=d_{1} \mathbf{v}_{1}+d_{2} \mathbf{v}_{2}\), then the linear combination of \(\mathbf{v}_{1}\), \(\mathbf{v}_{2}\), \(\mathbf{v}_{3}\) can be written as \(c_{1} \mathbf{v}_{1}+c_{2} \mathbf{v}_{2}+c_{3} \mathbf{v}_{3}=\left(c_{1}+d_{1}\right) \mathbf{v}_{1}+\left(c_{1}+d_{1}\right) \mathbf{v}_{2}\) which is also a linear combination of \(\mathbf{v}_{1}\), \(\mathbf{v}_{2}\).
8. Linear Dependence and Linear System Solution
Also, a linearly dependent set produces multiple possible linear combinations of a given vector.
Given a vector equation \(x_{1} \mathbf{v}_{1}+x_{2} \mathbf{v}_{2}+x_{3} \mathbf{v}_{3}=\mathbf{b}\), suppose the solution is \(\mathbf{x}=\left[\begin{array}{l}x_{1} \\ x_{2} \\ x_{3}\end{array}\right]=\left[\begin{array}{l}3 \\ 2 \\ 1\end{array}\right]\), i.e., \(3 \mathbf{v}_{1}+2 \mathbf{v}_{2}+1 \mathbf{v}_{3}=\mathbf{b}\).
Suppose also \(\mathbf{v}_{3}=2 \mathbf{v}_{1}+3 \mathbf{v}_{2}\), a linearly dependent case.
Then, \(3 \mathbf{v}_{1}+2 \mathbf{v}_{2}+1 \mathbf{v}_{3}=3 \mathbf{v}_{1}+2 \mathbf{v}_{2}+\left(2 \mathbf{v}_{1}+3 \mathbf{v}_{2}\right)=5 \mathbf{v}_{1}+5 \mathbf{v}_{2}\), so \(\mathbf{x}=\left[\begin{array}{l}x_{1} \\ x_{2} \\ x_{3}\end{array}\right]=\left[\begin{array}{l}5 \\ 5 \\ 0\end{array}\right]\) is another solution.
Actually, Many more solutions exist, e.g., \(3 \mathbf{v}_{1}+2 \mathbf{v}_{2}+1 \mathbf{v}_{3}=3 \mathbf{v}_{1}+2 \mathbf{v}_{2}+\left(2 \mathbf{v}_{3}-1 \mathbf{v}_{3}\right) =3 \mathbf{v}_{1}+2 \mathbf{v}_{2}+2\left(2 \mathbf{v}_{1}+3 \mathbf{v}_{2}\right)-1 \mathbf{v}_{3}=7 \mathbf{v}_{1}+8 \mathbf{v}_{2}-1 \mathbf{v}_{3}\), thus \(\mathbf{x}=\left[\begin{array}{l}x_{1} \\ x_{2} \\ x_{3}\end{array}\right]=\left[\begin{array}{c}7 \\ 8 \\ -1\end{array}\right]\) is another solution.