3. Linear Combination
1. 키워드
Linear Combination(선형결합): 벡터의 스칼라배들이 합으로 연결된 형태
Span(생성): 어떤 벡터 집합의 모든 선형결합의 집합
행렬의 곱셈
2. Linear Combinations
Given vectors \(\mathbf{v}_{1}, \mathbf{v}_{2}, \cdots, \mathbf{v}_{p}\) in \(\mathbb{R}^{n}\) and given scalars \(c_{1}, c_{2}, \cdots, c_{p}\) ,
\(c_{1} \mathbf{v}_{1}+\cdots+c_{p} \mathbf{v}_{p}\)
is called a linear combination of \(\mathbf{v}_{1}, \cdots, \mathbf{v}_{p}\) with weights of coefficients \(c_{1}, \cdots, c_{p}\) .
The weights in a linear combination can be any real numbers, including zero.
3. From Matrix Equation to Vector Equation
Recall the matrix equation of a linear system:
\[
\left[\begin{array}{lll}60 & 5.5 & 1 \\65 & 5.0 & 0 \\55 & 6.0 & 1\end{array}\right]\left[\begin{array}{l}x_{1} \\x_{2} \\x_{3}\end{array}\right]=\left[\begin{array}{l}66 \\74 \\78\end{array}\right]
\]
A matrix equation can be converted into a vector equation:
\[
\begin{gathered}
{\left[\begin{array}{l}
60 \\
65 \\
55
\end{array}\right] x_{1}+\left[\begin{array}{l}
5.5 \\
5.0 \\
6.0
\end{array}\right] x_{2}+\left[\begin{array}{l}
1 \\
0 \\
1
\end{array}\right] x_{3}=\left[\begin{array}{l}
66 \\
74 \\
78
\end{array}\right]} \\
\mathbf{a}_{1} x_{1}+\mathbf{a}_{2} x_{2}+\mathbf{a}_{3} x_{3}=\mathbf{b}
\end{gathered}
\]
4. Existence of Solution for \(A \mathbf{x}=\mathbf{b}\)
Consider its vector equation:
\[
\begin{gathered}{\left[\begin{array}{l}60 \\65 \\55\end{array}\right] x_{1}+\left[\begin{array}{l}5.5 \\5.0 \\6.0\end{array}\right] x_{2}+\left[\begin{array}{l}1 \\0 \\1\end{array}\right] x_{3}=\left[\begin{array}{l}66 \\74 \\78\end{array}\right]} \\\mathbf{a}_{1} x_{1}+\mathbf{a}_{2} x_{2}+\mathbf{a}_{3} x_{3}=\mathbf{b}\end{gathered}
\]
When does the solution exist for \(A \mathbf{x}=\mathbf{b}\) ?
5. Span
Definition : Given a set of vectors \(\mathbf{v}_{1}, \cdots, \mathbf{v}_{p} \in \mathbb{R}^{n}\) , \(\operatorname{Span}\left\{\mathbf{v}_{1}, \cdots, \mathbf{v}_{p}\right\}\) is defined as the set of all linear combinations of \(\mathbf{v}_{1}, \cdots, \mathbf{v}_{p}\) .
That is, \(\operatorname{Span}\left\{\mathbf{v}_{1}, \cdots, \mathbf{v}_{p}\right\}\) is the collection of all vectors that can be written in the form \(c_{1} \mathbf{v}_{1}+c_{2} \mathbf{v}_{2} \cdots+c_{p} \mathbf{v}_{p}\) with arbitrary scalars \(c_{1}, \cdots, c_{p}\) .
\(\operatorname{Span}\left\{\mathbf{v}_{1}, \cdots, \mathbf{v}_{p}\right\}\) is also called the subset of \(\mathbb{R}^{n}\) spanned (or generated ) \(\mathbf{v}_{1}, \cdots, \mathbf{v}_{p}\) .
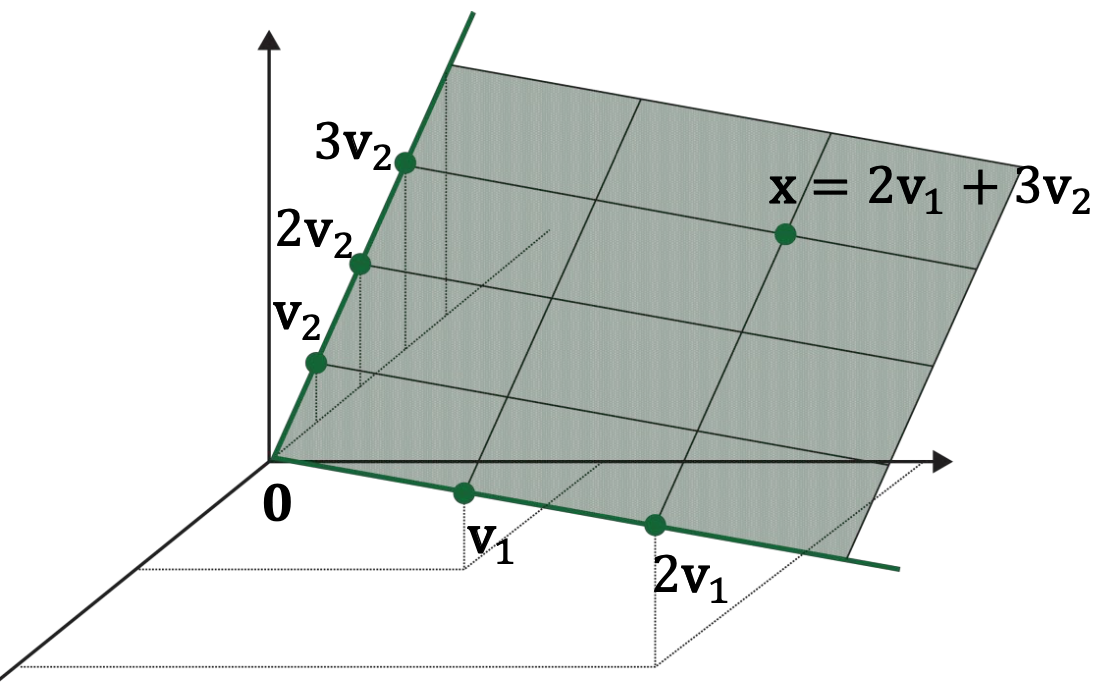
6. Geometric Description of Span
If \(\mathbf{v}_{1}\) are \(\mathbf{v}_{2}\) nonzero vectors in \(\mathbb{R}^{3}\) , with \(\mathbf{v}_{2}\) not a multiple of \(\mathbf{v}_{1}\) , then \(\operatorname{Span}\left\{\mathbf{v}_{1}, \mathbf{v}_{2}\right\}\) is the plane in \(\mathbb{R}^{3}\) that contains \(\mathbf{v}_{1}\) , \(\mathbf{v}_{2}\) and \(\mathbf{0}\) .
In particular, \(\operatorname{Span}\left\{\mathbf{v}_{1}, \mathbf{v}_{2}\right\}\) contains the line in \(\mathbb{R}^{3}\) through \(\mathbf{v}_{1}\) and \(\mathbf{0}\) and the line through \(\mathbf{v}_{2}\) and \(\mathbf{0}\) .
7. Geometric Interpretation of Vector Equation
Finding a linear combination of given vectors \(\mathbf{a}_{1}\) , \(\mathbf{a}_{2}\) , and \(\mathbf{a}_{3}\) to be equal to \(\mathbf{b}\) :
\[
\begin{gathered}{\left[\begin{array}{l}60 \\65 \\55\end{array}\right] x_{1}+\left[\begin{array}{l}5.5 \\5.0 \\6.0\end{array}\right] x_{2}+\left[\begin{array}{l}1 \\0 \\1\end{array}\right] x_{3}=\left[\begin{array}{l}66 \\74 \\78\end{array}\right]} \\\mathbf{a}_{1} x_{1}+\mathbf{a}_{2} x_{2}+\mathbf{a}_{3} x_{3}=\mathbf{b}\end{gathered}
\]
The solution exists only when \(\mathbf{b} \in \operatorname{Span}\left\{\mathbf{a}_{1}, \mathbf{a}_{2}, \mathbf{a}_{3}\right\}\) .
8. Matrix Multiplications as Linear Combinations of Vectors
Recall : We defined matrix-matrix multiplications as the inner product between the row on the left and the column on the right:
\[
\left[\begin{array}{cc}1 & 6 \\ {3} & {4} \\ 5 & 2\end{array}\right]\left[\begin{array}{cc}1 & -1 \\ {2} & 1\end{array}\right]=\left[\begin{array}{cc}13 & 5 \\ 11 & 1 \\ 9 & -3\end{array}\right]
\]
Inspired by the vector equation, we can view \(A \mathbf{x}\) as a linear combination of columns of the left matrix:
\[
\left[\begin{array}{lll}60 & 5.5 & 1 \\ 65 & 5.0 & 0 \\ 55 & 6.0 & 1\end{array}\right]\left[\begin{array}{l}x_{1} \\ x_{2} \\ x_{3}\end{array}\right]=A \mathbf{x}=\left[\begin{array}{lll}\mathbf{a}_{1} & \mathbf{a}_{2} & \mathbf{a}_{3}\end{array}\right]\left[\begin{array}{l}x_{1} \\ x_{2} \\ x_{3}\end{array}\right]=\mathbf{a}_{1} x_{1}+\mathbf{a}_{2} x_{2}+\mathbf{a}_{3} x_{3}
\]
9. Matrix Multiplications as Column Combinations
Linear combinations of columns
Left matrix: bases, right matrix: coefficients
One column on the right:
\[
\left[\begin{array}{ccc}1 & 1 & 0 \\1 & 0 & 1 \\1 & -1 & 1\end{array}\right]\left[\begin{array}{l}1 \\2 \\3\end{array}\right]=\left[\begin{array}{l}1 \\1 \\1\end{array}\right] 1+\left[\begin{array}{c}1 \\0 \\-1\end{array}\right] 2+\left[\begin{array}{l}0 \\1 \\1\end{array}\right] 3
\]
Multi-columns on the right:
\[
\begin{aligned}&{\left[\begin{array}{ccc}1 & 1 & 0 \\1 & 0 & 1 \\1 & -1 & 1\end{array}\right]\left[\begin{array}{cc}1 & -1 \\2 & 0 \\3 & 1\end{array}\right]=\left[\begin{array}{ll}x_{1} & y_{1} \\x_{2} & y_{2} \\x_{3} & y_{3}\end{array}\right]=[\mathbf{x} \mathbf{y}]} \\&\mathbf{x}=\left[\begin{array}{l}x_{1} \\x_{2} \\x_{3}\end{array}\right]=\left[\begin{array}{l}1 \\1 \\1\end{array}\right] 1+\left[\begin{array}{c}1 \\0 \\-1\end{array}\right] 2+\left[\begin{array}{l}0 \\1 \\1\end{array}\right] 3 \\&\mathbf{y}=\left[\begin{array}{l}y_{1} \\y_{2} \\y_{3}\end{array}\right]=\left[\begin{array}{l}1 \\1 \\1\end{array}\right](-1)+\left[\begin{array}{c}1 \\0 \\-1\end{array}\right] 0+\left[\begin{array}{l}0 \\1 \\1\end{array}\right] 1\end{aligned}
\]
10. Matrix Multiplications as Row Combinations
Linear combinations of rows of the right matrix
Right matrix: bases, right matrix: coefficients
One row on the left:
\[
\left[\begin{array}{lll}
1 & 2 & 3
\end{array}\right]\left[\begin{array}{ccc}
1 & 1 & 0 \\
1 & 0 & 1 \\
1 & -1 & 1
\end{array}\right]=\begin{aligned} 1 \times\left[\begin{array}{ccc}
1 & 1 & 0
\end{array}\right] \\
+2 \times\left[\begin{array}{ccc}
1 & 0 & 1
\end{array}\right] \\
+3 \times\left[\begin{array}{ccc}
1 & -1 & 1
\end{array}\right]
\end{aligned}
\]
Multiple rows on the left:
\[
\begin{aligned}&\left[\begin{array}{ccc}1 & 2 & 3 \\1 & 0 & -1\end{array}\right]\left[\begin{array}{ccc}1 & 1 & 0 \\1 & 0 & 1 \\1 & -1 & 1\end{array}\right]=\left[\begin{array}{lll}x_{1} & x_{2} & x_{3} \\y_{1} & y_{2} & y_{3}\end{array}\right]=\left[\begin{array}{l}\mathbf{x}^{\mathrm{T}} \\\mathbf{y}^{\mathrm{T}}\end{array}\right]\\&\mathbf{x}^{\mathrm{T}}=\left[\begin{array}{lll}x_{1} & x_{2} & x_{3}\end{array}\right]=1\left[\begin{array}{lll}1 & 1 & 0\end{array}\right]+2\left[\begin{array}{lll}1 & 0 & 1\end{array}\right]+3\left[\begin{array}{lll}1 & -1 & 1\end{array}\right]\\&\mathbf{y}^{\mathrm{T}}=\left[\begin{array}{lll}y_{1} & y_{2} & y_{3}\end{array}\right]=1\left[\begin{array}{lll}1 & 1 & 0\end{array}\right]+0\left[\begin{array}{lll}1 & 0 & 1\end{array}\right]+(-1)\left[\begin{array}{lll}1 & -1 & 1\end{array}\right]\end{aligned}
\]
11. Matrix Multiplications as Sum of (Rank-1) Outer Products
(Rank-1) outer product:
\[
\left[\begin{array}{l}1 \\1 \\1\end{array}\right]\left[\begin{array}{lll}1 & 2 & 3\end{array}\right]=\left[\begin{array}{lll}1 & 2 & 3 \\1 & 2 & 3 \\1 & 2 & 3\end{array}\right]
\]
Sum of (Rank-1) outer products:
\[
\begin{aligned}{\left[\begin{array}{cc}1 & 1 \\1 & -1 \\1 & 1\end{array}\right]\left[\begin{array}{lll}1 & 2 & 3 \\4 & 5 & 6\end{array}\right] } &=\left[\begin{array}{l}1 \\1 \\1\end{array}\right]\left[\begin{array}{lll}1 & 2 & 3\end{array}\right]+\left[\begin{array}{c}1 \\-1 \\1\end{array}\right]\left[\begin{array}{lll}4 & 5 & 6\end{array}\right] \\&=\left[\begin{array}{lll}1 & 2 & 3 \\1 & 2 & 3 \\1 & 2 & 3\end{array}\right]+\left[\begin{array}{ccc}4 & 5 & 6 \\-4 & -5 & -6 \\4 & 5 & 6\end{array}\right]\end{aligned}
\]
12. Matrix Multiplications as Sum of (Rank-1) Outer Products
Sum of (Rank-1) outer products is widely used in machine learning
Covariance matrix in multivariate Gaussian
Gram matrix in style transfer
References