20. 재귀호출(Recursive Call)
1. 키워드
- 재귀호출(Recursive Call)
- 최대 재귀 깊이(Maximum Recursion Depth)
2. 함수에서 재귀호출 사용하기
- 함수 안에서 함수 자기자신을 호출하는 방식을 재귀호출이라고 한다.
- 보통 알고리즘에 따라서 반복문으로 구현한 코드보다 재귀호출로 구현한 코드가 좀 더 직관적이고 이해하기 쉬운 경우가 많다.
3. 재귀호출 사용하기
def hello():
print("Hello, world!")
hello()
hello()
# Hello, world!
# Hello, world!
# Hello, world!
# ...(생략)
# RecursionError: maximum recursion depth exceeded while pickling an object
hello 함수 안에서 다시 hello 함수를 호출하고 있다.- 소스 코드를 실행해 보면
"Hello, world!" 문자열이 계속 출력되다가 에러가 발생한다.
- 왜냐하면 파이썬에서는 최대 재귀 깊이(Maximum Recursion Depth)가 1,000으로 정해져 있어서 그렇다.
- 즉,
hello 함수가 자기자신을 계속 호출하다가 최대 재귀 깊이를 초과하면 RecursionError가 발생한다.
- 재귀호출을 그림으로 나타내면 다음과 같은 모양이 된다.
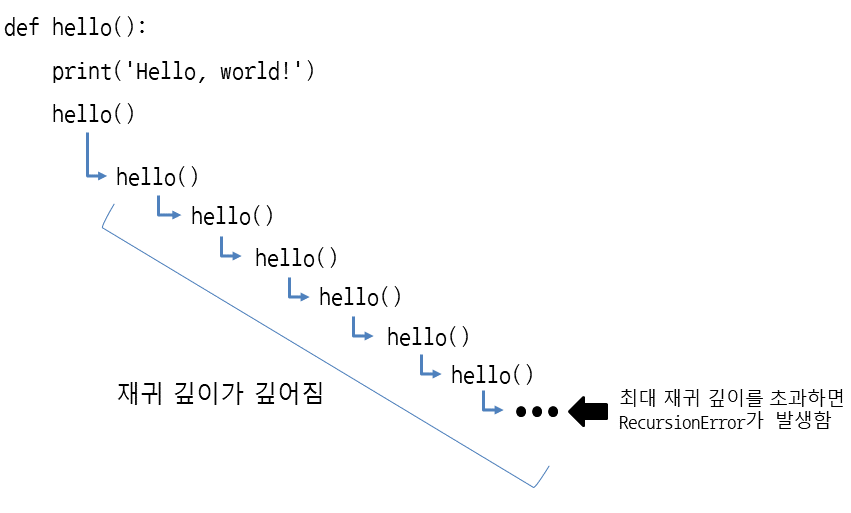
1) 재귀호출에 종료 조건 만들기
- 재귀호출을 사용하려면 반드시 다음과 같이 종료 조건을 만들어주어야 한다.
def hello(count):
if count == 0:
return
print("Hello, world!", count)
count -= 1
hello(count)
hello(5)
# Hello, world! 5
# Hello, world! 4
# Hello, world! 3
# Hello, world! 2
# Hello, world! 1
- 먼저
hello 함수의 반복 횟수를 계산하기 위해 매개변수 count를 지정한다.
- 그리고
count가 0이면 hello 함수를 호출하지 않고 끝낸다.
- 만약
0이 아니면 "Hello, world!"를 출력하고, count의 값을 1씩 감소시킨 뒤 hello 함수를 호출할 때 넣어준다.

4. 재귀호출로 팩토리얼 구하기
- 팩토리얼은
1부터 n까지 양의 정수를 차례대로 곱한 값이며 !(느낌표) 기호로 표기한다.
- 예를 들어
5!은 5 * 4 * 3 * 2 * 1이며 결과는 120이다.
def factorial(n):
if n == 1:
return 1
return n * factorial(n - 1)
print(factorial(5)) # 120
- 먼저
factorial 함수를 만들 때 매개변수 n을 지정해 준다.
- 팩토리얼은
1부터 n까지의 곱을 구하는 문제인데 여기서는 n부터 역순으로 1씩 감소하면서 재귀호출을 하고 n이 1이 되었을 때 재귀호출을 중단한다.
def factorial(n):
if n == 1:
return 1
factorial 함수의 핵심은 반환값 부분이다.- 계산 결과가 즉시 구해지는 것이 아니라 재귀호출로
n - 1을 계속 전달하다가 n이 1일 때 비로소 1을 반환하면서 n과 곱하고 다시 결괏값을 반환한다.
- 그 뒤
n과 반환된 결괏값을 곱하여 다시 반환하는 과정을 반복한다.
return n * factorial(n - 1)
factorial(5)를 호출해서 n이 1이 될 때까지 재귀호출하면 다음과 같은 모양이 된다.

- 이제
if n == 1:을 만나서 factorial 함수가 1을 반환한다.
- 그 뒤
1과 2를 곱해서 2를 반환하고, 3과 2를 곱해서 6을 반환하고, 4와 6을 곱해서 24를 반환하고, 5와 24를 곱해서 120을 반환하게 된다.

factorial 함수의 계산 과정을 그림 하나로 표현하면 다음과 같은 모양이 된다.

References




