3. 실수 자료형
1. 키워드
- 실수 자료형
- 부동소수점(Floating-Point)
2. 실수 자료형 사용하기
- 지금까지 정수를 변수에 저장했다.
- 이번에는 소수점을 표현할 수 있는 실수를 변수에 저장해 보자.
- 다음은 실수 자료형의 크기와 저장할 수 있는 값의 범위이다.

지수 표기법(Exponential Notation)
- 아주 큰 숫자나 아주 작은 숫자를 표기할 때는 지수 표기법을 사용한다.
- 지수 표기법은 과학적 표기법(Scientific Notation)이라고도 부른다.
1] 실수e+지수
실수*10의거듭제곱2.1e+3이라면2.1*1000 = 2100이 된다.
2] 실수e-지수
실수*(1/10의거듭제곱)2.1e-2라면2.1*(1/100) = 0.021이 된다.
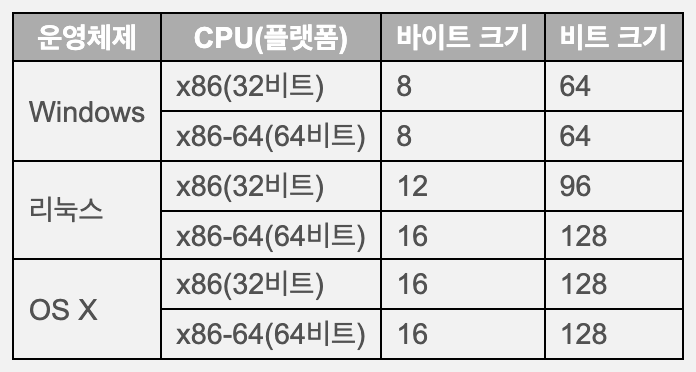
long double 타입
long double타입은 운영체제와 플랫폼마다 크기가 다르다.
- 지금부터 설명할 부동소수점 규약은 참고삼아 읽어보면 된다.
- 컴퓨터에서는 값을
0과1로 저장한다. - 그래서 실수도
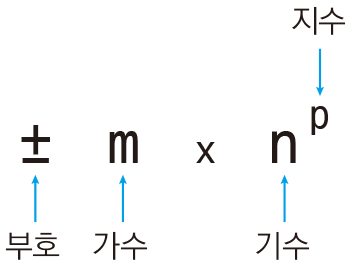
0과1로 저장해야 하는데 이렇게 실수와 소수점을 2진수로 표현하는 방식을 부동소수점 표현 방식이라고 한다. - 부동소수점 방식은 자료형의 일정 부분을 비트 단위로 나누어 부호, 가수(Significand), 기수(Base), 지수(Exponent)를 저장하여 실수를 표현한다.
- 부동소수점은 다음과 같이 기수(\(n\))를 지수(\(p\))만큼 거듭제곱한 값을 가수(\(m\))와 곱하는 방식을 사용한다.
- 단, 컴퓨터는 값을 저장할 때 2진수로 저장하므로 기수(밑수)는 2로 고정되어 있으며 2 자체는 따로 저장하지 않는다.
- 부동소수점 저장에 관한 규약은 IEEE 754라는 표준으로 정해져 있다.
- 다음은 IEE 754에서 단정밀도 부동소수점인
float타입과 배정밀도 부동소수점인double타입의 저장 방식이다.

- 유효자릿수는 실수를 일정 자릿수만큼만 표현할 수 있다는 뜻이다.
- 만약 유효자릿수가
7이라면0.123456789는 반올림하여0.123457로 표시된다. - 즉, 정수 부분
1자리와 소수 부분6자리로7자리가 표시된다. - 단정밀도와 배정밀도 부동소수점은 저장할 수 있는 크기가 다르므로 유효자릿수의 차이가 있다.
- 따라서 배정밀도 부동소수점이 좀 더 긴 자릿수의 소수점을 정밀하게 표현할 수 있다.
3. 실수형 변수 선언하기
- 다음 내용을 입력한 뒤 실행해 보자.
#include <stdio.h>
int main()
{
// 단정밀도 부동소수점 변수를 선언하고 값을 할당
// float 타입은 숫자 뒤에 f를 붙임
float num1 = 0.1f;
// 배정밀도 부동소수점 변수를 선언하고 값을 할당
// double 타입은 숫자 뒤에 아무것도 붙이지 않음
double num2 = 3867.215820;
// 배정밀도 부동소수점 변수를 선언하고 값을 할당
// long double 타입은 숫자 뒤에 l을 붙임
long double num3 = 9.327513l;
// float과 double 타입은 %f로 출력, long double 타입은 %Lf로 출력
printf("%f %f %Lf\n", num1, num2, num3); // 0.100000 3867.215820 9.327513
return 0;
}
- 소수점을 사용하여 실수를 저장해 봤다.
- 단, 소수점을 사용해서 표기해도 변수 안에 저장될 때는 IEEE 754 부동소수점 방식으로 저장된다.
- 여기서
float타입은 숫자 뒤에f나F를 붙여주고,long double타입은l이나L을 붙여준다. double타입은 아무것도 붙이지 않는다.- 그리고
1.f,.1f처럼 소수점 앞 또는 뒤의0은 생략할 수 있다. float과double타입을printf로 출력할 때는 서식 지정자로%f를 사용하고,long double타입을 출력할 때는%Lf를 사용한다.
- 이번에는 지수 표기법으로 실수를 저장해 보자.
#include <stdio.h>
int main()
{
// 지수 표기법으로 300000을 표기
// float 타입은 숫자 뒤에 f를 붙임
float num1 = 3.e5f;
// 지수 표기법으로 -0.013827을 표기
// double 타입은 숫자 뒤에 아무것도 붙이지 않음
double num2 = -1.3827e-2;
// 지수 표기법으로 5210000000을 표기
// long double 타입은 숫자 뒤에 l을 붙임
long double num3 = 5.21e+9l;
// float과 double 타입은 %f로 출력, long double 타입은 %Lf로 출력
printf("%f %f %Lf\n", num1, num2, num3); // 300000.000000 -0.013827 5210000000.000000
// 지수 표기법으로 출력할 때는 float과 double 타입은 %e로 출력
// long double 타입은 %Le로 출력
printf("%e %e %Le\n", num1, num2, num3); // 3.000000e+05 -1.382700e-02 5.210000e+09
return 0;
}
- 지수 표기법으로 표기할 때는 정수 부분은 한 자릿수만 적고, 소수자릿수 뒤에
e와 지수를 표기한다. - 마찬가지로 변수 크기에 맞게 마지막에
f또는l을 붙여준다. e뒤에 지수가 양수이면 소수점 기준으로 자릿수가 왼쪽으로 이동하며, 음수이면 오른쪽으로 이동한다.- 지수가 양수일 때는
+를 생략할 수 있다. printf함수는 실수를 지수 표기법으로 출력할 수도 있다.float과double타입은%e로,long double타입은%Le로 출력하면 된다.
4. 자료형 크기 구하기
- 이번에는 각 실수 자료형의 크기를 구해 보자.
#include <stdio.h>
int main()
{
float num1 = 0.0f;
double num2 = 0.0;
long double num3 = 0.01l;
printf("float: %d, double: %d, long double: %d\n",
sizeof(num1), // sizeof로 float 타입 변수의 타입 크기를 구함
sizeof(num2), // sizeof로 double 타입 변수의 타입 크기를 구함
sizeof(num3)); // sizeof로 long double 타입 변수의 타입 크기를 구함
return 0;
}
// float: 4, double: 8, long double: 16
float타입은 4바이트,double타입은 8바이트,long double타입은 16바이트이다.
5. 최솟값과 최댓값 표현하기
- 이번에는 실수 자료형의 양수 최솟값과 최댓값을 표현하는 방법을 알아보자.
#include <stdio.h>
#include <float.h> // 실수 자료형의 양수 최솟값, 최댓값이 정의된 헤더 파일
int main()
{
float num1 = FLT_MIN; // float 타입의 양수 최솟값
float num2 = FLT_MAX; // float 타입의 양수 최댓값
double num3 = DBL_MIN; // double 타입의 양수 최솟값
double num4 = DBL_MAX; // double 타입의 양수 최댓값
long double num5 = LDBL_MIN; // long double 타입의 양수 최솟값
long double num6 = LDBL_MAX; // long double 타입의 양수 최댓값
printf("%.40f\n", num1);
printf("%.2f\n", num2);
printf("%e %e\n", num3, num4);
printf("%Le %Le\n", num5, num6);
return 0;
}
// 0.0000000000000000000000000000000000000118
// 340282346638528859811704183484516925440.00
// 2.225074e-308 1.797693e+308
// 3.362103e-4932 1.189731e+4932
float.h헤더 파일에 각 자료형 별로 양수 최솟값과 최댓값이 정의되어 있다.printf함수에서 서식 지정자를%.40f,%.2f처럼 소수점 뒤에 숫자를 지정하면 해당 숫자만큼 소수점 이하 자릿수를 출력한다.double,long double타입의 최소, 최댓값은 소수점 이하 자리가 매우 길기 때문에printf함수에서 서식 지정자로%e,%Le를 사용하여 지수 표기법으로 출력해 봤다.
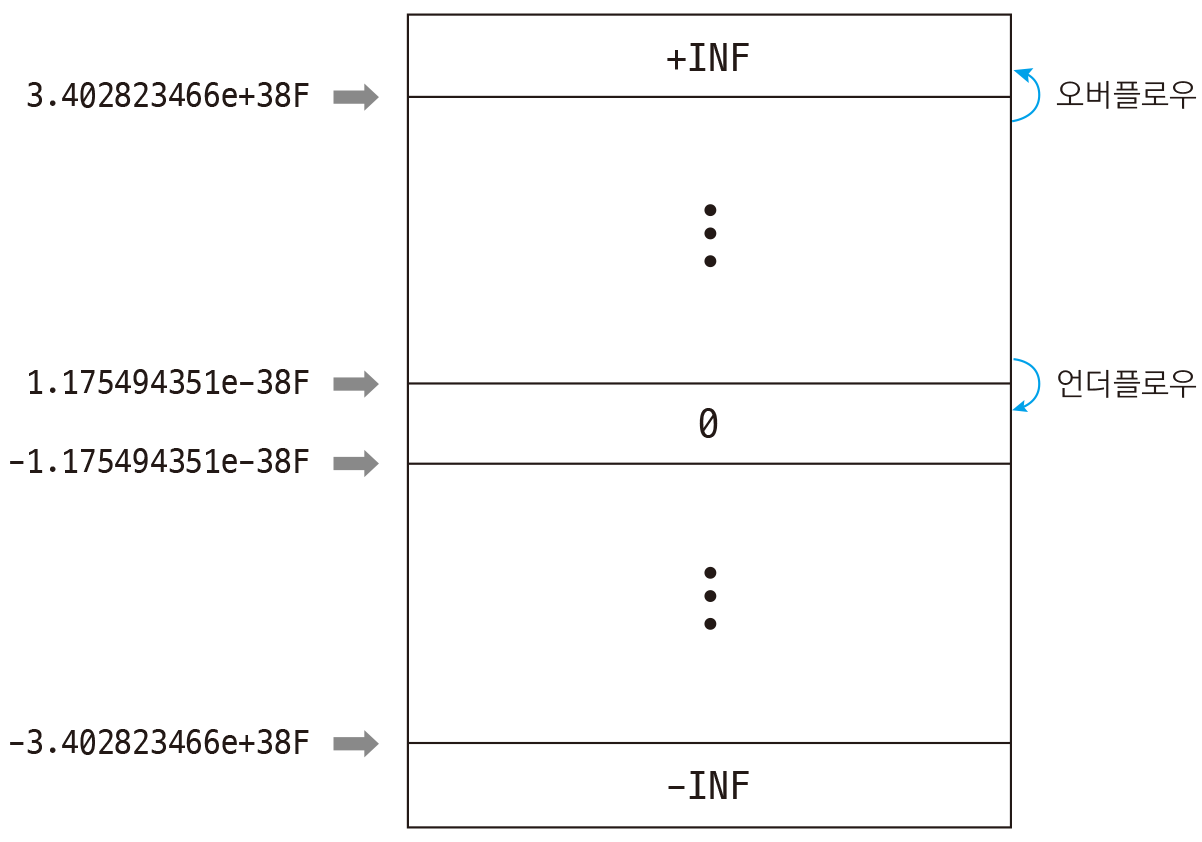
6. 오버플로우와 언더플로우 알아보기
- 정수 자료형과 마찬가지로 실수 자료형도 오버플로우와 언더플로우가 발생할 수 있다.
#include <stdio.h>
#include <float.h> // 실수 자료형의 양수 최솟값, 최댓값이 정의된 헤더 파일
int main()
{
float num1 = FLT_MIN; // float 타입의 양수 최솟값
float num2 = FLT_MAX; // float 타입의 양수 최댓값
// float 타입의 양수 최솟값을 100000000.0으로 나누면 아주 작은 수가 되면서 언더플로우 발생
num1 = num1 / 100000000.0f;
// float 타입의 양수 최댓값에 1000.0을 곱하면 저장할 수 있는 범위를 넘어서므로 오버플로우 발생
num2 = num2 * 1000.0f;
// 0.000000e+00 inf: 실수의 언더플로우는 0
// 오버플로우는 무한대가 됨
printf("%e %e\n", num1, num2); // 0.000000e+00 inf
return 0;
}
FLT_MIN을100000000.0과 같이 큰 수로 나누면 아주 작은 수가 되면서 언더플로우가 발생하는데 C에서는 실수 언더플로우를0또는 쓰레기 값으로 처리한다.- 반대로
FLT_MAX에1000.0을 곱하면 저장할 수 있는 범위를 넘어서기 때문에 오버플로우가 발생한다. - 정수와는 달리 실수는 오버플로우가 발생했을 때 최솟값으로 돌아가지 않고 무한대(Infinity)가 되므로
inf가 출력된다.