15. 벡터의 내적(Dot Product)
1. 벡터의 연산
벡터(Vector)는 기본적으로 합(Summation)과 곱(Multiplication)이라는 두 가지 연산을 기반으로 작용한다. 벡터의 합은 서로 다른 두 벡터를 더하는 개념이고, 벡터의 곱은 크게 3종류로 나뉜다. 첫 번째는 주어진 하나의 벡터를 늘이거나 줄이는 "스케일링(Scaling)", 두 번째는 서로 다른 두 벡터를 곱 연산했을 때 결과가 스케일러(Scalar)가 되는 내적(Dot product), 세 번째는 서로 다른 두 벡터를 곱 연산했을 때 결과가 벡터가 되는 외적(Cross product)이 있다. 내적과 외적은 근본적으로 벡터의 합과 곱(스케일링)을 기반으로 하며, 이러한 합과 곱을 선형결합(Linear combination)이라고 한다.
2. 내적(Dot Product)
벡터의 내적이 구성되려면 기본적으로 동일한 차원에 존재하는 벡터 두 개를 고려한다. 예를 들어, \(\overrightarrow{\mathrm{V}}\)와 \(\overrightarrow{\mathrm{W}}\)이 주어졌을 때 두 벡터의 내적은 \(\overrightarrow{\mathrm{V}} \cdot \overrightarrow{\mathrm{W}}\)와 같이 표기한다.
2차원의 경우 각각의 벡터는 2개의 성분을 가지고 있으므로 \(\left[\begin{array}{l}a \\b\end{array}\right] \cdot\left[\begin{array}{l}c \\d\end{array}\right]=a c+b d\)와 같이 표기되며, 이 내적의 계산 방법은 각각의 벡터의 성분끼리 곱해서 더하면 된다.
여기서 "성분끼리 곱해서 더한다"의 기하학적 의미는 한 벡터를 다른 벡터로 투영(projection)하는 것과 관련이 있다. 투영에 대해 생각해 보면 순서와 상관 없이 두 벡터 중 하나의 벡터를 기준으로 잡고 나머지 한 벡터를 기준 벡터가 존재하는 관점으로 재해석한다는 의미가 된다.
예를 들어, 2차원의 기저벡터(Basis vector) \(\hat{\mathrm{i}}\), \(\hat{\mathrm{j}}\)의 도착지가 \(\left[\begin{array}{ll}2 & 1 \\0 & 0\end{array}\right]\)인 선형변환 행렬이 있다. 즉, \(T (\hat{\mathrm{i}}) = \left[\begin{array}{ll}2 \\0 \end{array}\right]\), \(T (\hat{\mathrm{j}}) = \left[\begin{array}{ll}1 \\0 \end{array}\right]\) 을 의미한다.
기저벡터의 도착지의 y 좌표 값이 모두 0이기 때문에 \(\left[\begin{array}{ll}2 & 1 \\0 & 0\end{array}\right]\)와 같이 표현되지만, 이런 경우 2차원의 속성을 그대로 가지고 있는 것처럼 보인다. 또한 기저벡터의 도착지가 \(\left[\begin{array}{ll}2 & 1 \\0 & 0\end{array}\right]\)인 경우 어떠한 벡터라도 x축 위를 벗어날 수 없게 된다. 이런 경우 차라리 \(\left[\begin{array}{ll}2 & 1 \\0 & 0\end{array}\right]\)이 아니라 \(\left[\begin{array}{ll}2 & 1\end{array}\right]\)로 표현하는 것이 좋아 보인다.
기저벡터의 도착지가 \(\left[\begin{array}{ll}2 & 1\end{array}\right]\)이라는 것은 1차원 직선상에 있는 두 점을 의미한다. 0을 표기한다는 것은 y축 성분을 그대로 고려하겠으나 값이 없음을 나타내는 의미이고, 0이 없이 표기된 것은 y축 자체를 정의하지 않겠다는 의미가 된다. 이 경우 \(\left[\begin{array}{ll}2 & 1\end{array}\right]\)이라는 선형변환 행렬은 2차원을 1차원으로 차원을 낮춘 행렬이 된다. 즉, 2차원 위에 표현된 모든 점들을 1차원으로 뭉개는 행렬이다.
다음 그림을 보면, 이는 2차원 벡터를 어떠한 선형변환에 의해 \(\hat{\mathrm{u}}\)와 나란한 직선(1차원)에 투영한 결과를 나타낸다.
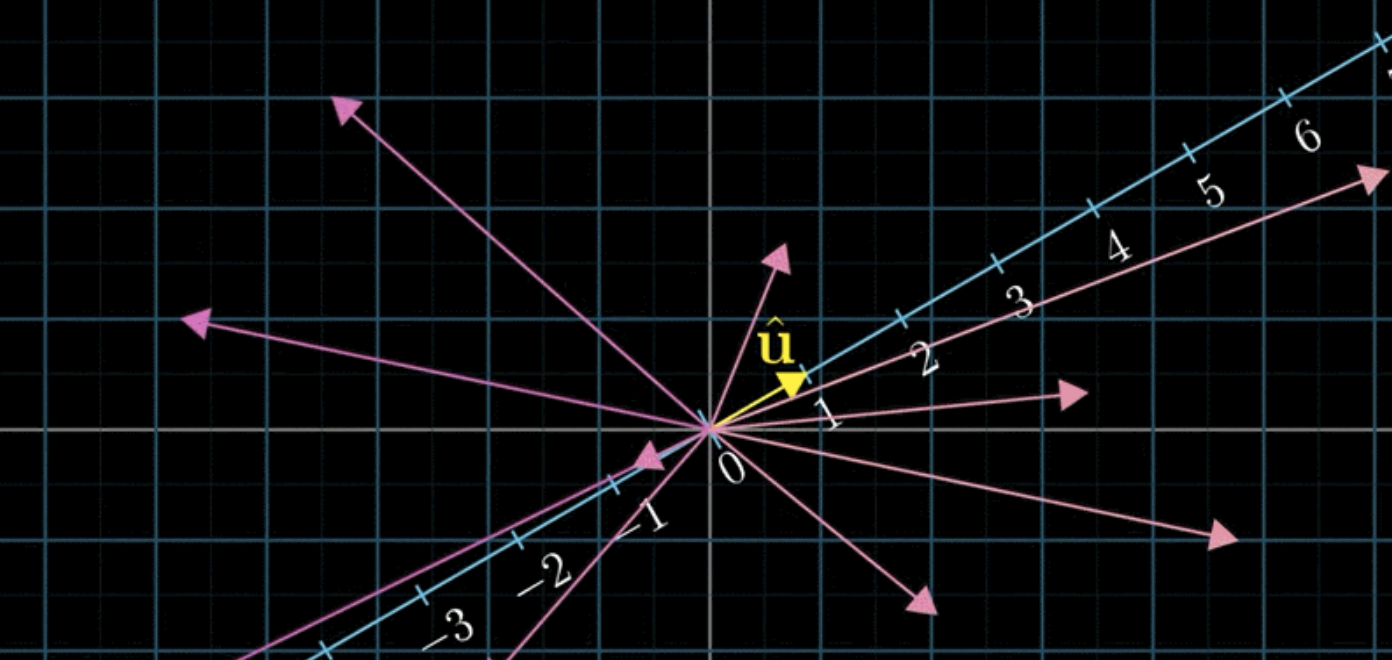

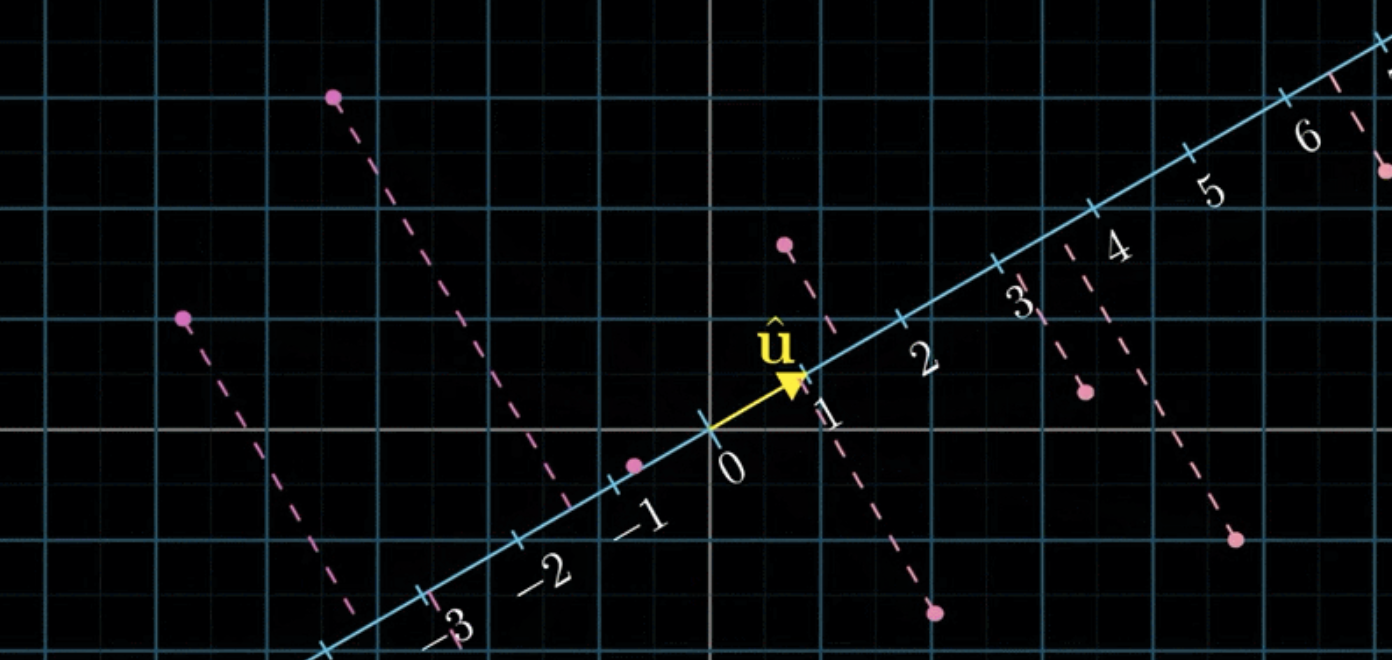
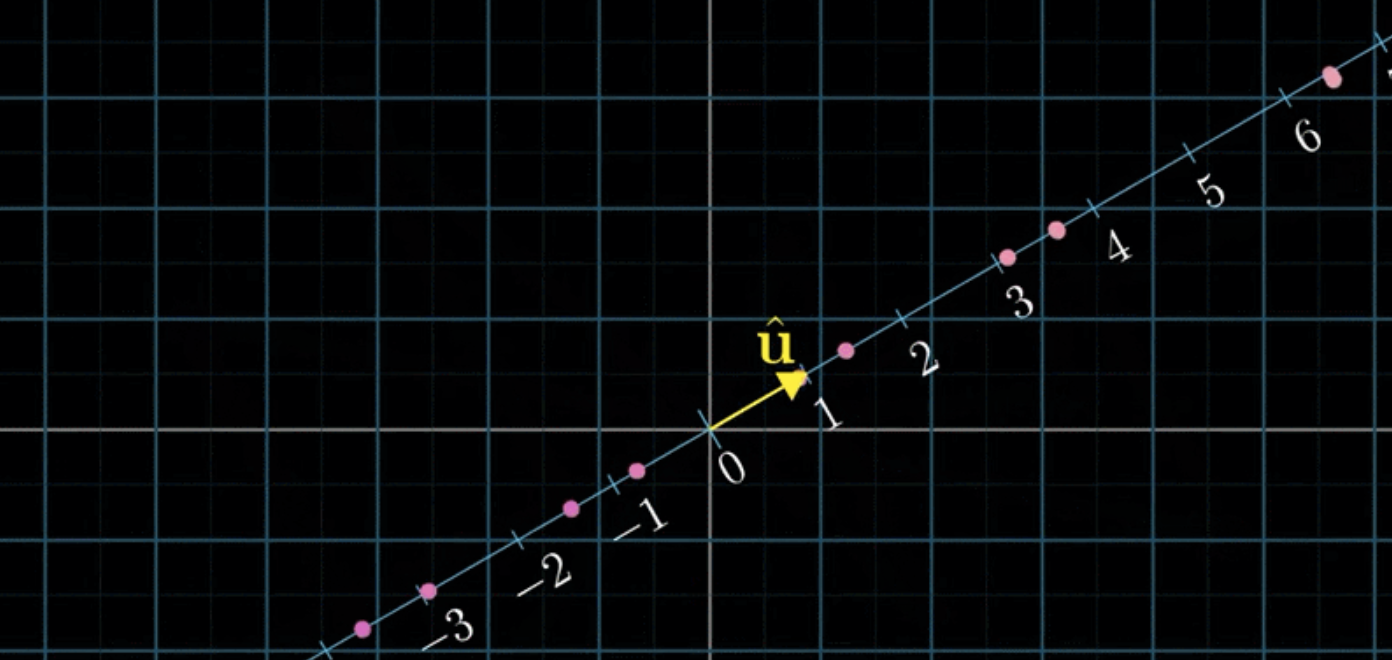
이것 또한 마찬가지로 2차원의 정보를 1차원(스케일러)으로 정의한 선형변환이 된다. 이와 같이 2차원의 세계를 \(\hat{\mathrm{u}}\)가 살고 있는 1차원의 세계로 환원하는 선형변환 행렬은 기본적으로 \(1 \times 2\) matrix로 나타내진다. 다음 그림을 보고 투영(projection)을 나타내는 선형변환을 찾아보자.
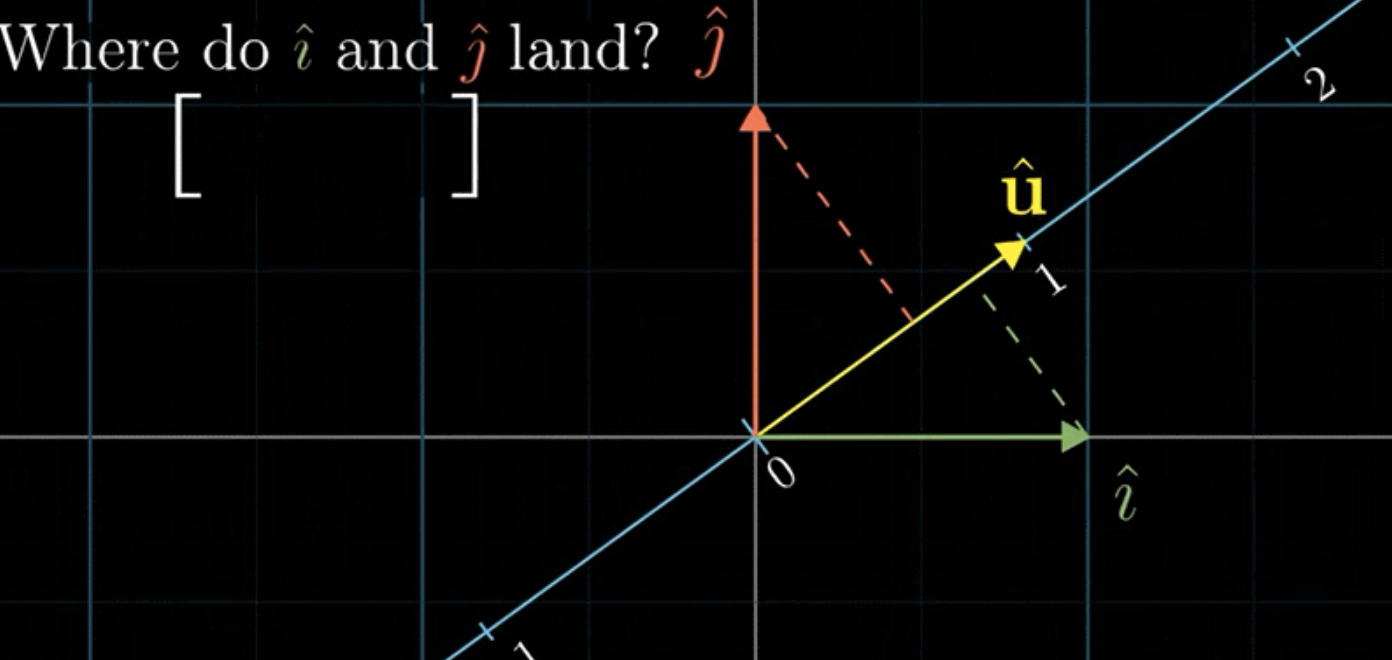
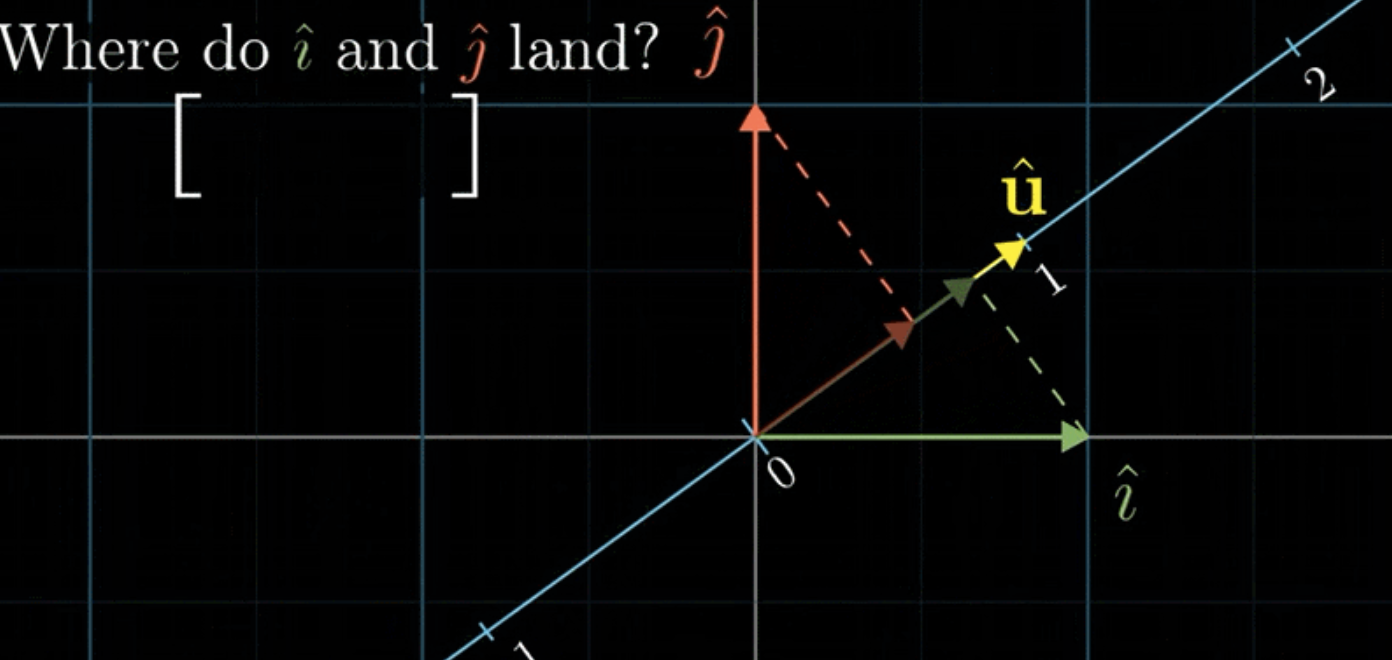
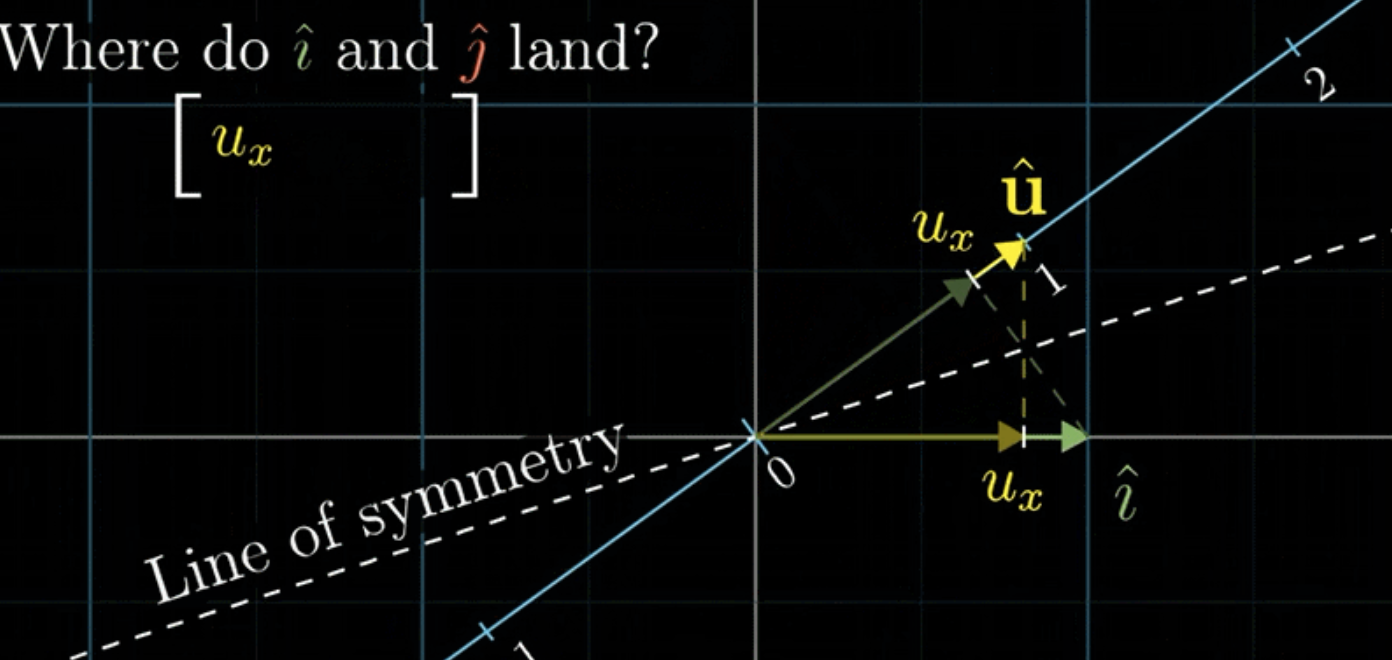

선형변환은 기저벡터의 도착지점이 해당 선형변환의 정보를 알려준다. 대칭성에 의해 \(\hat{\mathrm{i}}\)와 \(\hat{\mathrm{j}}\)를 각각 1차원의 \(\hat{\mathrm{u}}\)로 투영한 결과는 \(\hat{\mathrm{u}}\)를 각각 2차원의 x축과 y축에 투영한 결과와 같기 때문에 2차원에서의 \(\hat{\mathrm{u}}\)의 x 및 y 좌표임을 알 수 있다. 이는 곧 어떤 벡터의 \(\hat{\mathrm{u}}\) 벡터로의 투영을 나타내는 선형변환 행렬 \(\left[\begin{array}{ll}\mathrm{u}_x & \mathrm{u}_y\end{array}\right]\)을 의미한다.
내적은 두 벡터 중 하나의 벡터를 기준으로 잡고 나머지 한 벡터를 기준 벡터로의 투영을 의미한다. 위에서 어떤 벡터로의 투영을 나타내는 선형변환은 그 벡터 자체의 좌표가 됨을 확인했다. 만약 성분 \(c\), \(d\)를 가지는 어떤 벡터를 성분 \(a\), \(b\)를 가지는 다른 벡터로의 투영은 \(\left[\begin{array}{ll}a & b\end{array}\right]\left[\begin{array}{l}c \\d\end{array}\right]\)와 같이 쓸 수 있다. 이는 또한 성분 \(a\), \(b\)를 가지는 어떤 벡터를 성분 \(c\), \(d\)를 가지는 다른 벡터로의 투영인 \(\left[\begin{array}{ll}c & d\end{array}\right]\left[\begin{array}{l}a \\b\end{array}\right]\)와 동일하다.